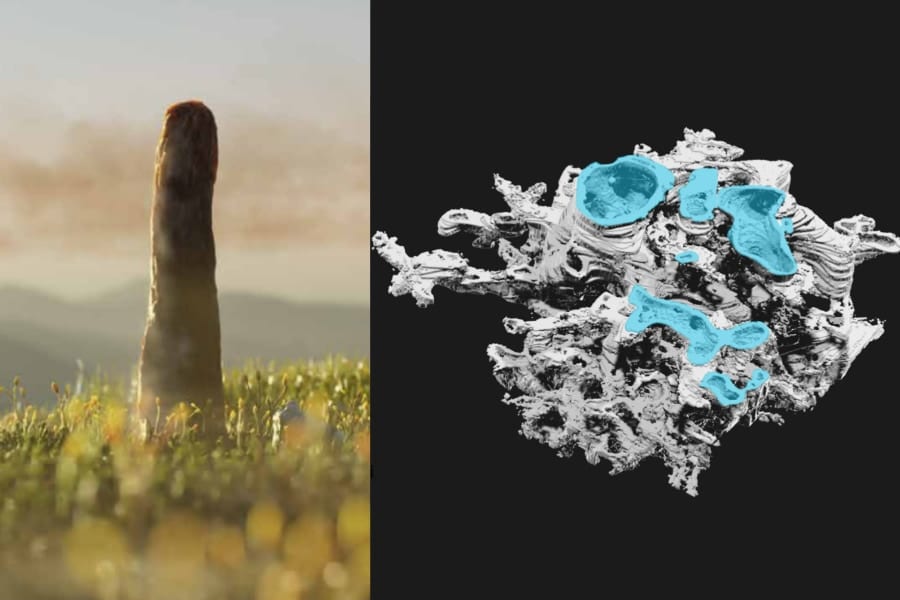
ドラゴン型の3面サイコロを設計できる
では研究チームはどのようにして、物体が止まる向きを計算しているのでしょうか？
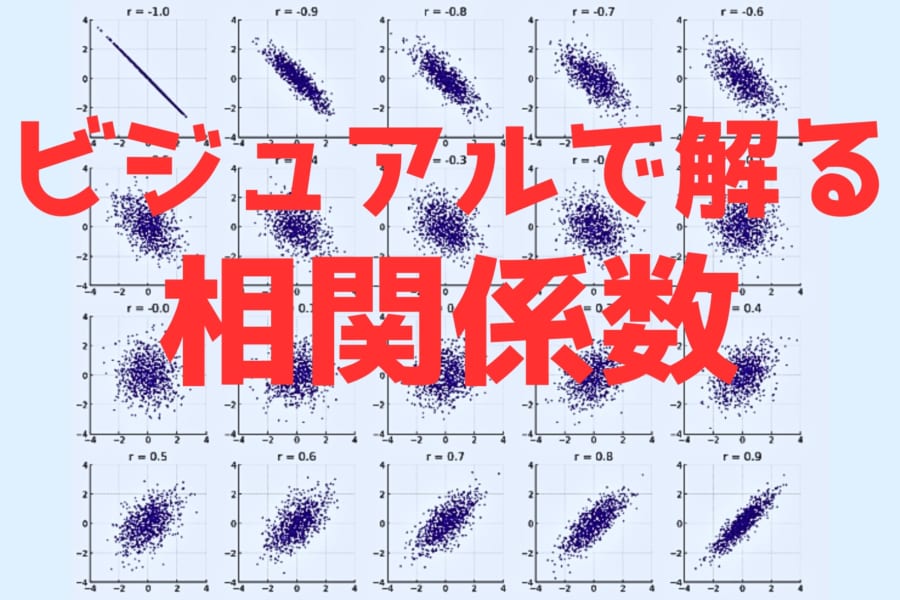
ポイントは重心の高さと凸包（とつほう）です。
物体が転がって最終的に安定するのは、重力によって重心ができるだけ低くなる向きで止まるためです。
言い換えれば、重心の位置が他より低い姿勢は安定しやすく、それが物体の「出目」に相当します。
研究チームはまず物体の形状全体を外側から包む最小の凸型の多面体（凸包）を考え、次にその凸包が各面・辺・頂点で地面と接したときに物体がどんな向きになるかを系統立てて整理しました。
具体的には、物体を様々な角度に傾けた際に重心の高さがどう変化するかを単位球上にマッピングします（ガウス写像と呼ばれる手法）。
球面上のある点は物体の特定の向きを意味し、その点の高さに対応する重心の高さを計算することで、「どの向きで重心が最低になるか」「その向きでは物体のどの部分が下になるか」がわかるのです。
この重心高さの分布（球面上の関数）を解析し、傾きに応じて物体が転がっていく経路をすべて追跡すれば、初期のランダムな向きから出発して最終的にどの面で安定するかの確率を計算できます。
こうした純粋に幾何学にもとづく計算法により、従来の物理シミュレーションに比べ大幅な高速化が達成されました。
研究論文によれば、計算速度は従来比で単純な形状では約400倍、複雑な形状でも60倍にもなり、たとえばブタの形をした玩具サイコロ（有名なパーティーゲーム「Pass the Pigs」ではブタのミニチュアを振って出目を競います）の6通りの静止パターンと確率もわずか0.003秒（3ミリ秒）で計算できたと報告されています。
これほど高速であれば、リアルタイムに近い形でデザイン中のモデルの安定性をチェックすることも夢ではありません。
研究チームは次に、この計算法を応用した「逆問題」に取り組みました
なわち、「指定した確率で止まるサイコロの形状を自動で設計する」という挑戦です。
研究チームはこの発想を実装し、確率と頂点座標の勾配をリアルタイムで計算できる設計ツールを開発しました。
例えば、「コイン2枚を投げたときと同じ確率で表の枚数が出る3面体」や、「6面ダイス2個の合計と同じ確率分布を持つ11面体」（出目2～12が出る確率がちょうど2個サイコロの場合と一致する）をこのアルゴリズムで自動生成できることを示しています。
つまり多少形が複雑でも等確率化できるサイコロにでき、逆に好きなように確率を偏らせた不公平なサイコロも作れるわけです。
従来の職人芸的なバランス調整では到底見つけられないような形状のサイコロも、この方法なら発見できると研究者らは述べています。
実際、古典的なサイコロ設計では避ける「追加の不安定な面」をあえて持たせることで、見た目が自然なのに狙った確率でしか止まらないサイコロ形状など、ユニークな例が数多く示されました。
研究チームはこうして設計した「特殊サイコロ」を3Dプリンターで実際に造形し、物理的に転がして結果を検証しました。
例えば、ネコやアルマジロの立体モデルをベースに、それぞれ3つの安定面を持つサイコロに変形したものがあります。
そのほかドラゴン型やウサギ型など様々な形状で、公平・不公平含め思い通りの確率特性を持たせることに成功しました。
実験では、こうした造形サイコロを実際に300～1000回ほど繰り返し転がして統計を計測しました。
その結果、多くの試作品で理論計算どおりの確率分布に非常に近い実測結果が得られ、手法の有効性が確認されました。
例えば「2個のサイコロ合計を再現する11面体」を転がした実験でも、出目2～12の出現頻度が期待値にほぼ合致したとのことです。
計算による事前予測が、そのまま現実のサイコロにも適用できたわけです。
ただし、転がす際にあまり強くバウンドすると、跳ね方など運動量の影響で予測からズレる場合も観察されました。
（※思い切り地面に叩きつけるような異常なバウンドをすると、ドラゴン型サイコロの足や翼などがモデル予測を超えた曲がりや反発が起こるためだと考えられます）
またモデル予測の精度は100%にはまだ届いておらず、全体で3～4％程度のズレもみられました。
この点について研究チームは、今後より精緻なモデルで改善していきたいと述べています。
