14歳が「1万倍の重さに耐える折り紙」構造を発見、2万5千ドル獲得

14歳少年が「ミウラ折り」で災害シェルターの課題に挑む

ウーさんが目を向けたのは、山火事やハリケーンなどの自然災害です。

ニュースで被災地の様子を知るうちに、「現地で使われる仮設テントやシェルターには課題が多いのではないか」と考えるようになりました。

災害用のシェルターには、少なくとも3つの条件が求められます。

1つ目は「強くて壊れにくいこと」、2つ目は「小さく畳めて運びやすいこと」、3つ目は「現場ですぐに展開できること」です。

ところが現実には、この3つを同時に満たす構造はなかなか見つかりません。

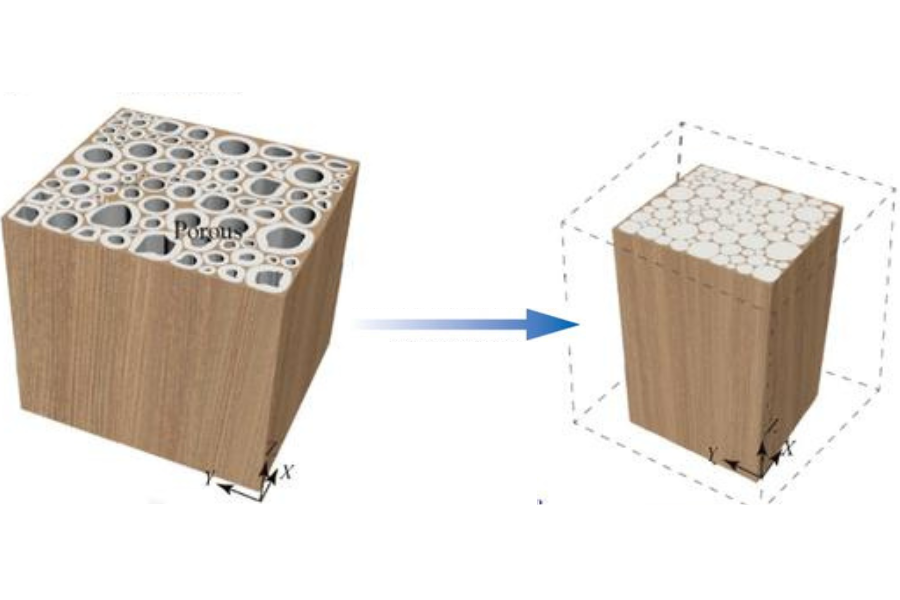
そこで彼が目を付けたのが「ミウラ折り」です。

ミウラ折りは、同じ形の平行四辺形を格子状につないだように折り筋を入れることで、シート全体を蛇腹のように一気に畳んだり広げたりできる折り方です。

薄く平らに畳める一方で、一度広げると凸凹のある立体的な面が現れます。

この性質から、実際に人工衛星の太陽電池パネルの収納・展開などにも利用されています。

ウーさんは、子どものころから趣味で折り紙を続けてきましたが、最近は自分で折り方を設計するようになっていました。

その延長で、「この折り方の形そのものに、力学的な強さが隠れているのではないか」と考えたのです。

 

この投稿をInstagramで見る

 

Society for Science(@society4science)がシェアした投稿

彼はミウラ折りの形を決めるパラメータに注目しました。

具体的には、平行四辺形の幅（パネルの横方向の大きさ）、平行四辺形の角度、折り上がりの高さ、使用する紙の種類といった要素を組み合わせて条件を変え、合計54種類のミウラ折り構造を作りました。

そしてそれぞれについて耐荷重試験を行っています。

では、その地道なテストから、どんな結果が得られたのでしょうか。