ダイソン球を安定化させる新理論
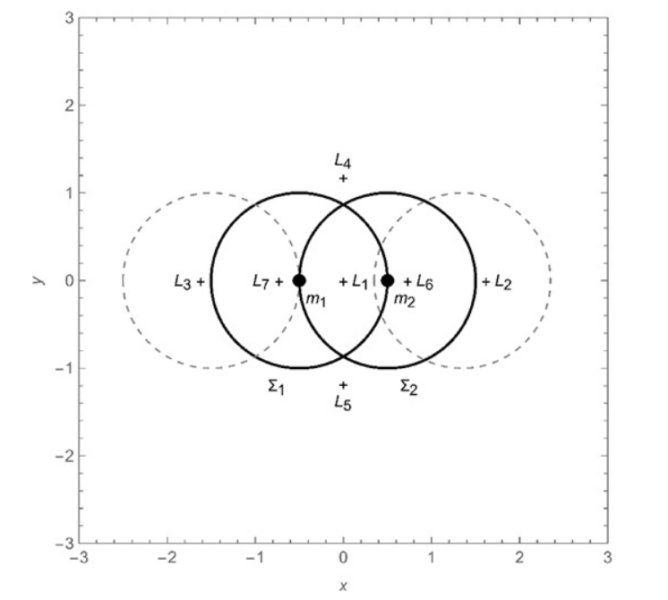
調査にあたってはコンピュータ上で“仮想の宇宙”を作り出してシミュレーションを行いました。
イメージとしては「二つの星がぐるぐる回っている状況」に「とても大きいけれど羽のように軽いリング（または球殻）」をそっと置いてみるわけです。
二つの星は互いの重力で引き合って回転し、リングや球殻はそこから受ける引力を頼りに「どこに落ち着こうとするのか」、あるいは「少しでも揺らすとすぐに転げ落ちてしまうのか」を見るのです。
実際にやってみると、あたかも何本もの綱引きロープの真ん中にリングや球殻を据えたような状態になることがわかります。
もし星がひとつしかないと、少し引っ張られればあとはドミノ倒しのように崩れてしまいます。
ところが二つの星がちょうどいい位置関係で引っ張り合っていると、リングや球殻が引かれる向きが多方向から微妙に均衡するため、まるで“ぐらぐらだけど倒れない”シーソーの真ん中に乗っているような状態が生まれるわけです。
研究チームはこの均衡点を時間をかけてシミュレーションし、ほんの少し揺らしてみても大崩壊せずに安定するパターンが存在するのを確認しました。
特に印象的なのは、「小さいほうの星を取り囲むようにリングや球殻を配置すると、意外にも長い間崩れずに維持できる」という発見です。
通常の二体問題では「中心が恒星なら、そこから外れた瞬間に終わり」という話だったのに、連星系の場合は「小さな星を取り囲む」ことで、全体の重力のバランスがうまくいく可能性があるのです。
ただし、これは一定の質量比やリング・シェル半径など、パラメータが限られる上での結果であることも同時に示されています。
いわば、片側だけの綱引きではすぐに引きずられてしまうところを、もう片方の星も加わることで複数方向から引っ張られ、かえって“どっちにも行けない安定域”に落ち着く――そんなイメージです。
もちろん、この結果だけで「ダイソン球が当たり前のように存在するはずだ！」というわけではありません。
「恒星を覆う構造は不安定だ」という従来の常識に対して、“連星系という舞台ならそうとも限らない”という可能性を提示した点は大きいでしょう。
