「フェルマーの最終定理」とはどんな問題か?

「私はこの命題について、真に驚くべき証明を見出したが、それを記すにはここはあまりに余白が足りない」
360年前、フランスの数学者ピエール・ド・フェルマーはたったこれだけのメモを問題の脇に書き残してこの世を去ってしまいました。
フェルマーは今で言うところの承認欲求がまるでない人物でした。
自分で見つけた発見を世の中で認めてもらおうとはまったく考えず、1人で答えを見つけて1人で満足し喜んでいるだけだったのです。
しかし、そんなフェルマーの誰にも教えなかった「真に驚くべき証明」は、「フェルマーの最終定理」として数世紀先の時代まで彼の名を轟かせることになります。
難問とされながらもフェルマーの最終定理が一般にも非常に有名なのは、子供でも理解できる極めて単純な問いかけにあります。
フェルマーは、「xn + yn = zn という式のnが3以上のとき解がない(つまり絶対に式が成立しなくなる)」と言っています。
しかし、この式のnが2の場合、それは誰もが中学校で習う「ピタゴラスの定理(三平方の定理)」になります。
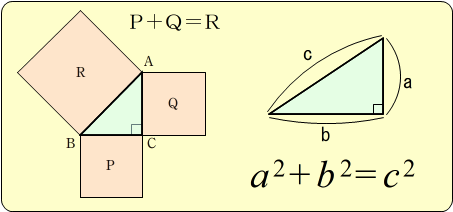
つまり「n=2」であれば、この「xn + yn = zn」という式を成立される「X,Y,Z」の解はたくさん存在するのです。それが「nが3以上」なった途端まったく成立しなくなるというのは、なんだかおかしな気がします。
例えば命題に含まれるように、nを3にして考えてみましょう。この場合、式は2つの異なる立方体の体積の和で新しくもっと大きな立方体が作れるか? という計算をしていることになります。
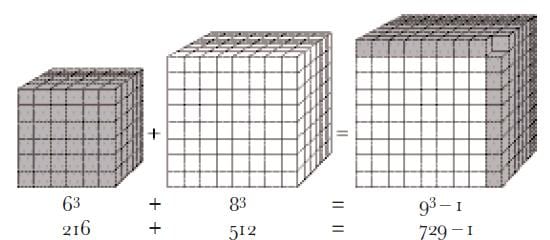
順々に数を当てはめて見ると、上の画像のように「6の3乗」と「8の3乗」を足したとき、「9の3乗より1少ない」という答えが出てきます。
非常におしい答えです。この調子ならすぐに成立する3つのX,Y,Zの組み合わせが見つかりそうな気もします。
ところが、そんな数はいくら探してもまったく見つからないのです。
ピタゴラスの定理に無限の解が存在する証明は、紀元前の数学者エウクレイデスが著書「原論」の中で紹介しています。
同じ式でnが2の場合、無限に解が存在すると証明できるなら、その逆に3以上で解が存在しないと証明することはそんなに難しくないような気がしてしまいます。
最終的にフェルマーの最終定理を証明したアンドリュー・ワイルズは、10歳のときにこの問題を図書館で見つけ、なぜ多くの数学者がこんな問題につまずいているのだろうか? と不思議に思いました。
きっと何か重要な鍵を見落としているだけで、あっさり証明できるんじゃないかと幼少時代のワイルズは思ったのです。
しかし、それは他の多くの数学者たちが落ちた危険な落とし穴でした。以後ワイルズは30年以上、この問題の呪縛に捕らわれることになります。


























![[W.P.S.] 防水スプレー 除菌 抗菌 防汚 機能付き 大容量420ml 日本製](https://m.media-amazon.com/images/I/41aHfy9uuZL._SL500_.jpg)

![[WILL CLENS] シューズパウダー 日本製 無香料 シューケアキット 靴 消臭 パウダー (1本)](https://m.media-amazon.com/images/I/41m8Ig2XigL._SL500_.jpg)
![よーく聞いてね!3つのヒントで学ぶ!どうぶつカード ([バラエティ])](https://m.media-amazon.com/images/I/51zT3OcliFL._SL500_.jpg)