パウリの排他原理
古典物理学では光も電子も手に負えないということが徐々に明らかになり、物理の世界は新しい理論を求めるようになっていました。
こうした中登場したのが、量子力学の歴史を語る上で欠かすことのできない重要人物の一人、ヴォルフガング・パウリです。
彼はかなり早熟の天才でした。世の中には「授業中に机の下に隠した漫画を読んでいた」なんて不届きな人もいるかも知れませんが、パウリの場合、退屈な授業中に隠れて読んでいたのは、アインシュタインの相対性理論の論文だったといいます。
彼の最初の師となったのは、前回話した、ボーアの原子モデルに電子軌道が楕円という修正を加えて完成形に近づけたゾンマーフェルトでした。
ゾンマーフェルトは数理科学百科事典という物理をまとめた本を作っていて、相対性理論の解説をアインシュタインに依頼しましたが断られたため、まだ19歳だったパウリにその編集を任せました。
パウリの書いた相対性理論の解説は完璧な出来栄えで、ゾンマーフェルトが「自分が直すところは何もない」と驚くほどでした。それは後日アインシュタイン本人も読むことになり、その深い洞察に称賛を送ったといいます。
そんなパウリでしたが、根っからの理論物理学者で、実験は大の苦手。実験器具もよく壊していたといいます。そのうち近づくだけで器具が壊れると噂され、科学と無縁のこの現象は冗談めかしてパウリ効果などと呼ばれました。
パウリはその後いくつかの研究室を渡り歩き、ボーアの講演に感銘を受けて、コペンハーゲンの研究所へ行くことになります。パウリの研究所滞在は1年という期限付きのものでしたが、ボーアとの付き合いはこの後生涯に渡って続きます。
一方この頃、ボーアは電子殻モデルというものを発表します。
授業中、机の下に隠して相対性理論を読んだりしなかった人なら、化学の授業で原子にはK殻、L殻、M殻などの殻があって、それぞれに入れる電子の数が2個、8個、18個と決まっているという話を聞いた覚えがあると思います。
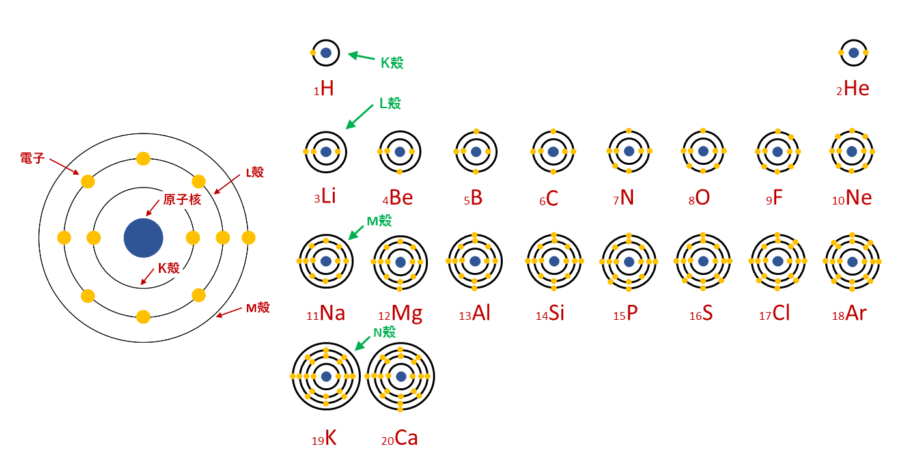
このモデルでは、最外殻電子の数によってなぜ周期的に元素に似た性質が現れるのかという、元素周期表の並びの意味を見事に説明していました。
電子殻はそれぞれ決められた上限の電子数があり、いっぱいになると殻が閉じて化学的に極めて安定した状態になります。
けれどボーアは相変わらず、経験的なデータからインスピレーションに頼ってこれを導いていて、なぜこのように電子殻の電子数が決定されるのか説明することはできませんでした。
恩師のラザフォードも優れたアイデアであることは認めつつも、「なぜ君がこの結論に至ったのかがまるで理解できない」と困惑したといいます。
しかし、ボーアはこのモデルをもとに当時未発見だった、元素番号72番の性質について予想を述べ、それは後に発見されたハフニウムと一致します。このためボーアの電子殻モデルは無視できない理論となりました。
このモデルに論理的な基礎を与えるヒントは、ラザフォードの研究室にいた大学院生エドマンド・ストーナーが発見します。
ボーア・ゾンマーフェルトの原子モデルでは、電子のエネルギー準位を決定するために、軌道の大きさ(n)、軌道の形(k)、軌道の向き(m)という3つのパラメータ（量子数）を使っていました。
ストーナーはこの3つの量子数を使って計算すると、それぞれの電子殻で電子が取ることのできるエネルギー状態が、1個、4個、9個に決定できるということを発見するのです。そして電子殻に入る電子の数はこのエネルギー状態の2倍の数になっていることを示したのです。
パウリはこの研究をヒントにして、現代まで彼の名を轟かせる「パウリの排他原理」を思いつきます。
電子は軌道上で、あるエネルギー状態を作りますが互いに同じエネルギー状態に入ることができません。それが電子殻に入れる電子数に上限を生み出しているのです。
しかし電子殻の上限は、なぜ電子の取りうるエネルギー状態数の2倍になってしまうのでしょう？
パウリはこの原因が、実は電子のエネルギー状態を決定するパラメータを1つ見落としているためではないかと考えます。
彼はこのとき、磁場の影響で線スペクトルが分裂する「異常ゼーマン効果」の原因解明に苦しんでいましたが、この問題を解決する鍵がその磁場に影響される新しいパラメータ（電子の自由度）だと気づくのです。
そして、パウリはそのパラメータに二価性という名を付けて導入します。
これは電子のエネルギー状態をさらに2つに分けることができました。つまり、ストーナーの計算したエネルギー状態の2倍が電子数の上限という問題が解決され、電子殻に関する基礎理論が完成したのです。
