もう一人の天才 ハイゼンベルク
パウリと同世代で、重要な物理学者がもう一人存在します。それがヴェルナー・ハイゼンベルクです。
ハイゼンベルクはもともとは数学者になろうとしていましたが、数学の教授とうまく行かず、父の紹介で出会った物理学者ゾンマーフェルトのもとで勉強することになります。
このときゾンマーフェルトの研究室には、パウリも在籍していました。ここでの出会いをきっかけに二人は生涯を通じた物理学研究の盟友となります。
量子論の魅力をハイゼンベルクに教えたのもパウリでした。

その後、ハイゼンベルクはパウリと同様ボーアの講義に感銘を受け、量子論の道を歩む決心をします。
そして、博士号取得後は、ゾンマーフェルトの紹介で、マックス・ボルンの助手として彼の研究室に入りました。
マックス・ボルンは、数学者から論理物理学者へ転向した人物で、この時代、ボーア、ゾンマーフェルトと並んで量子力学の重要人物でした。
ボルンは、そのとき、次々に見つかる新事実に物理学はもう1から全部作り直すしか無いだろうと考えていました。そして、その新理論を量子力学と呼んだのです。
ボルンの研究室に入ったハイゼンベルクは、原子核の周りを回る電子について考え始めます。
この当時、ハイゼンベルクはひどい花粉症を患っていて、ある時期は顔が腫れ上がって目も開けられないという状態になりました。
研究にも集中できないので、彼は仕方なく休暇をとって、花粉の届かない北海の小島ヘルゴラントへ旅行にいきます。そして、やっと訪れた落ち着いた環境の中でゆっくりと思考を巡らせた彼は、量子力学を確立させる大発見をするのです。
もともと数学を志していたハイゼンベルクは、観測できないものに視覚的イメージを持たせることはナンセンスだと考えていました。原子核の周りを軌道を描いて回る電子というイメージも、ハイゼンベルクにとってはひどく馬鹿馬鹿しいものだったのです。
彼は、物質の構成は観測できる値とその関係性だけで数学的に表現できるだろう、というちょっと小難しい考え方をしていました。
そこでハイゼンベルクは、電子がエネルギー準位間を瞬間的にジャンプするとき生じる線スペクトルの振動数など、観測で得られる値を全部書き出し、ボーアの対応原理によって量子的な値を古典的な運動量と位置に変換しました。
そして、そこから電子の振る舞いを計算しようとしたのですが、この複雑な式は運動量pと位置qを入れ替えて掛け算できないという、特殊な性質を持ってしまいました。
これはつまり、A×BとB×Aという計算をした場合、答えが異なってしまうということです。これを非可換性といいますが、掛け算の順序で答えが異なる計算というのをハイゼンベルクはそれまで経験したことがありませんでした。
ハイゼンベルクは悩みましたが、この成果をボルンに見せます。するとボルンは、「君がやっているのが行列計算だ」と言ったのです。
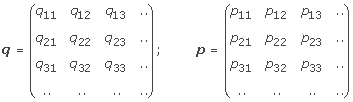
行列計算は、計算の順序を変えると答えも変わってしまいます。この当時、行列計算は数学では確立されていたものの、論理物理学者にはほとんど知られていませんでした。
数学に熟達したボルンは、この式を洗練させていき、まだ若手のヨルダンという研究者も引き込んで、ハイゼンベルクとともに三者論文と呼ばれることになる論文をかきあげました。
その論文は当時、ボーアに見せても「行列だらけで何がなんだかワケがわかりません」と言われたくらいです。
しかし、パウリはここで語られる理論を使って、水素原子の線スペクトルを論理的に再現することに成功します。
こうしてハイゼンベルクの傑作と言える、新しい物理学『行列力学』が誕生するのです。
けれど、何を計算しているのかイメージすることもできず、しかもなれない複雑で難解な行列計算を強いるこの行列力学は、同業の物理学者たちからはすこぶる評判が悪いものになりました。
物理学者たちは、行列力学が正しい結果を導けるため、仕方なくイヤイヤ受け入れるという状況になってしまったのです。
しかしこの行列力学の、運動量と位置という2つの物理量の非可換性(入れ替えて計算できない)は、2つの確定値を同時に得られないという不確定性原理の発見に結びついていくのです。
































![[AriRi] アップルウォッチ バンド シリコン ラバーバンド スポーツ くすみカラー 38mm 40mm 42mm 44mm 41mm 45mm 49mm アップルウォッチ 8 ultra se 7 6 5 4 3 2 1 全機種 全サイズ対応 (42mm/44mm/45mm/49mm, ブラック)](https://m.media-amazon.com/images/I/314SEY0tjsL._SL500_.jpg)

























