ゴールドバッハ予想
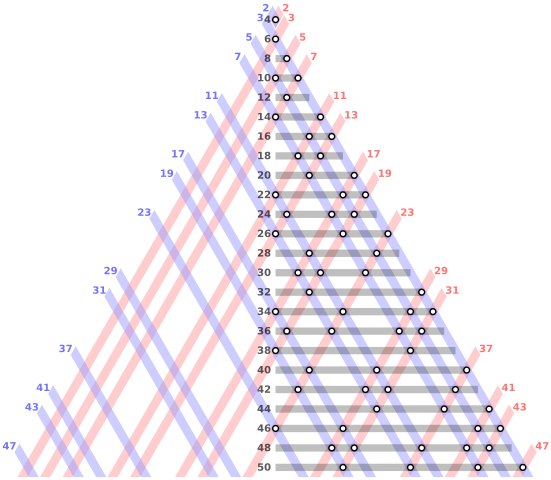
素数とは「1 より大きい整数で、正の約数が 1 と自分自身だけのもの」のことです。例えば、2 や 3 や 5 は素数ですが、6 は 2 と 3 を約数に持つので素数ではありません。
では、ゴールドバッハ予想の具体例を見てみましょう。
4 = 2+2
6 = 3+3
8 = 3+5
10 = 5+5 = 3+7
12 = 5+7
14 = 3+11 = 7+7
このように「4 以上の偶数は、必ず二つの素数の和で表すことができるだろう」というのがゴールドバッハ予想です。ぜひ、16 以上の偶数でも確認してみてください。
ゴールドバッハ予想は非常にシンプルな予想ですが、250 年以上も未解決の問題です。4000000000000000000（400京） 以下の偶数で、この予想が成立することがコンピュータで確認されています。
しかし、どれだけ大きな数まで、予想の成立を確認できても、予想が証明されたことにはなりません。なぜならば、その先に反例(予想が成立しない例)が存在する可能性があるからです。
ゴールドバッハ予想が相手にしているのは「全ての偶数」。無限に存在しています。どんなに大きな数でも、結局は無限に比べたら小さな有限の数でしかありません。
![ラボン(Lavons) 柔軟剤 特大 シャイニームーン[フローラルグリーン] 詰め替え 3倍サイズ 1440ml](https://m.media-amazon.com/images/I/41ze0Blp9fL._SL500_.jpg)
![ラボン(Lavons) 柔軟剤 特大 ラグジュアリーリラックス [アンバーウッディ] 詰め替え 3倍サイズ 1440ml](https://m.media-amazon.com/images/I/51Zp8NVKaAL._SL500_.jpg)
![シルバーバック【カンタン！たのしい！水の生きもの砂絵セット】 幼稚園 小学校 入園 入学 お祝い プレゼント 準備 ([バラエティ])](https://m.media-amazon.com/images/I/515gZ4F-QYL._SL500_.jpg)
