それは存在確率の波
いろいろ無理のあったシュレーディンガーの解釈に代わってボルンが考えたのは、波動関数が抽象的な可能性を表しているというものでした。
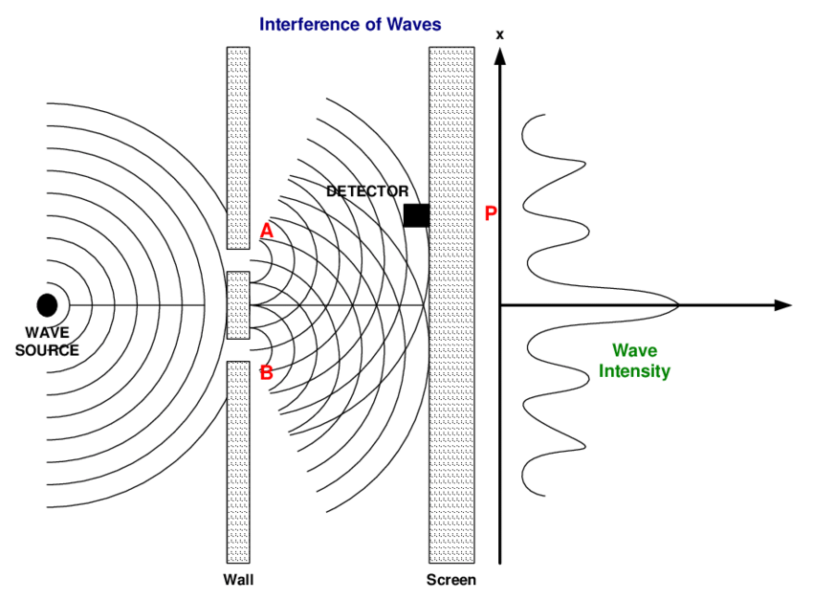
広がる波を計算している以上、波動関数からは電子の実際の位置は得られません。
では、我々は一体何を計算しているのかと言うと、それは電子がどこで見出されるかという確率なのだとボルンはいうのです。
ある地点Xとある地点Yで、波動関数を計算したとき、Yの方が値が大きいとすれば、それはYで電子が見出される可能性が高いことになります。
しかし、電子はXで見出されるかもしれないし、YでもXでもない場所で見出されるかもしれません。
シュレーディンガーの計算していた波とは、物理的に実在するものではなく、そこに電子があるかもしれないという存在確率の分布だとボルンは主張したのです。
しかし、これはシュレーディンガーにとっては受け入れがたい解釈でした。
物理学の世界は基本的に因果律に支配された決定論で記述されています。
例えばビリヤードで白ボールを別のボールにぶつけた場合、どのくらいの力でどの角度からぶつけたかによって、ボールが弾かれる方向と勢いは決まっています。
しかし、ボルンの解釈を当てはめてしまうと、ボール同士をぶつけたときに、どちらの方向へどのくらいの勢いで弾かれるのかは、確率でしか言及できず、いずれの状態になるか事前にはわからないことになるのです。
そんな馬鹿なことがあるわけない、というのがシュレーディンガーの考えでした。
なにより、せっかく自分が抽象的な電子の振る舞いを、連続して滑らかにつながる物理的な波として視覚的に表現し直したというのに、ボルンは再びそれを不連続で抽象的なものに戻してしまったのです。
そして、この確率解釈については、シュレーディンガー同様、納得していない人物がいました。それがアインシュタインです。
因果律と決定論を放棄する確率解釈は、アインシュタインにとってもありえないものでした。
だから彼はこういったのです。「神はサイコロを振らない」と。
ここから、量子力学は世界でもっとも成功した理論と言われながらも、その解釈を巡っては物理学の偉人たちが真っ向から対立し合う、奇妙な戦国時代に突入していくのです。
