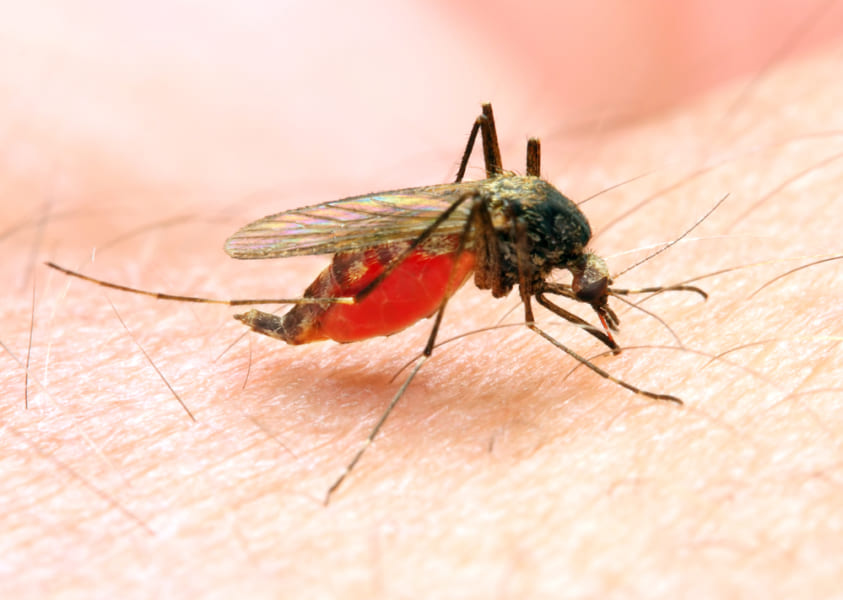
シュレーディンガー方程式は一体何を計算しているのか?
物質波を計算する波動方程式を見つけ出し、一世を風靡したシュレーディンガーでしたが、彼自身わかっていない問題がありました。
それはシュレーディンガー方程式が具体的には現実の何の波を計算しているのか? ということでした。
シュレーディンガーの波動方程式は、波動関数ψという波の、ある時刻tにおける、任意の点xの波の形を教えてくれます。
しかしシュレーディンガー自身、この波動関数ψが何を表しているのかわかりませんでした。
波といっているけれど、それは一体何が波打っているんだろう? それはシュレーディンガーを含め、みんなの疑問でした。
水の波は、上下運動する水分子の集団的な動きです。音波も、それは空気中の分子が波打って伝わっているものです。
波はその運動を伝える媒質が存在しなければ成り立ちません。
しかし、シュレーディンガー方程式の計算する物質波は、電子1つの波という古典物理学的な理解では意味不明なものを計算しています。
シュレーディンガーはこれを「電子の電荷が雲のように広がったものだ」という解釈をしました。
波動方程式が表しているものは、ある時刻tの任意の場所xにおける電荷の密度だ、というのが彼の考えでした。
では、数々の実験結果が示す粒子としての電子はなんなのでしょう?
シュレーディンガーはこれを、物質波のピークになった部分を我々が粒子と捉えているだけだと説明しました。
物質波は空間の至るところへ広がって、さまざまな波長の波が干渉を起こしています。それは束ね合わさって波束を作ります。その波束のピークが我々には粒子に見えるのだというのです。
あろうことかシュレーディンガーは、物質波を成立させるために、粒子なんて本当は存在しないと主張したのです。
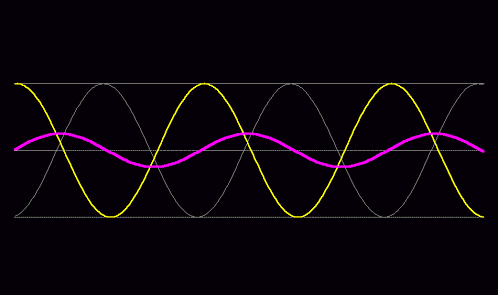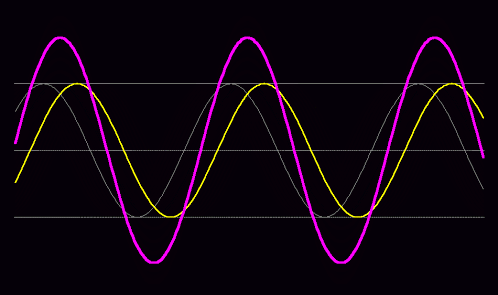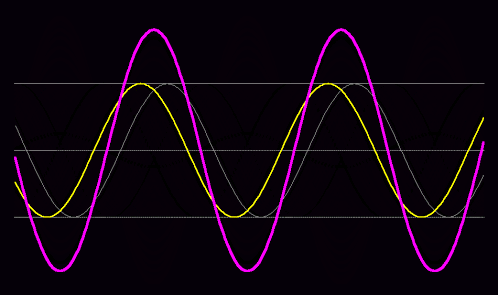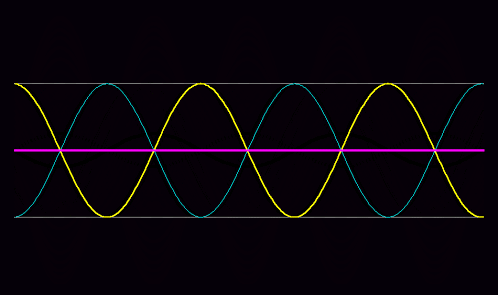
しかしこの理屈だと、波のピークはいくつもできるので、1つの電子が2つや3つに分裂して観測されても良いということになってしまいます。
どうして電子は1つのポイントに収束するのでしょう?
さらに、波動関数には、水素のような電子1つの場合はいいけれど、ヘリウムのように電子2つを含んだ原子の場合、3次元空間に2つの波があるという記述にならず、次元を足し合わせて6次元空間に存在する1つの波として記述してしまうという性質がありました。
これは電子が原子内に1つ増えるたびに、計算する次元が3つ増えるという恐ろしい状態を作り、ウランの波動関数に至っては276次元空間の波という記述になるのです。
これは物質波がシュレーディンガーの期待したような明快な実在の波ではなく、非常に抽象的な多次元空間の波であることを示していました。
それにシュレーディンガーの説明では、結局粒子性の証拠であるプランクの放射法則も光電効果もコンプトン効果も説明できないのです。
そのため、ボルンにも「シュレーディンガーの偉業は結局数学なのであって、彼の物理学はかなりお粗末だ」と言われてしまいます。
しかし、シュレーディンガーの波動関数が実在の三次元空間の波でないのだとしたら、この波は一体何を表しているのでしょうか?
マックス・ボルンは、この問題に対して、歴史に名を残す重要な解釈を提唱します。
それは、波動関数の確率解釈と呼ばれるものでした。




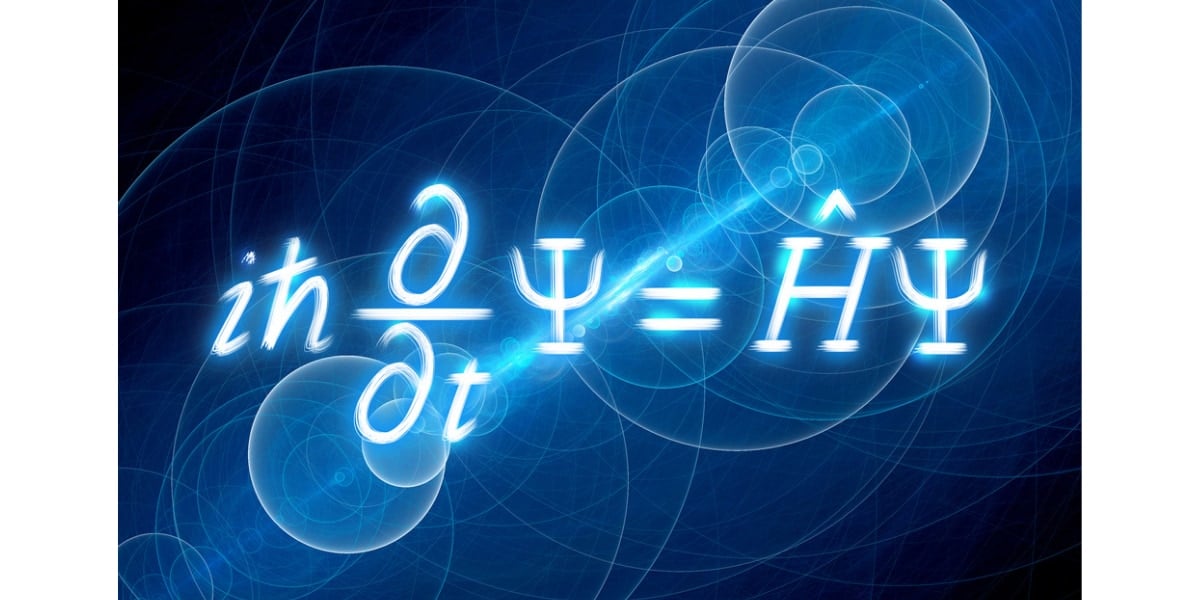
























![大人のさらさ 洗濯洗剤 ジェル 1900g シルクエッセンス効果で高保湿 ホワイトティー&フローラルの香り 詰め替え [大容量]](https://m.media-amazon.com/images/I/41G92luj2YL._SL500_.jpg)


![[コロンブス] キレイな状態をキープ アメダス 撥水・防水・防汚スプレー420mL](https://m.media-amazon.com/images/I/31-OcmTs2LL._SL500_.jpg)