重力が加速現象であることをすでに知っていた
研究主任のモリー・ガーリブ（Mory Gharib）氏は2017年に、レオナルドのデジタル化された実験ノートを閲覧していた際、ページの余白に小さな三角形のスケッチを発見しました。
スケッチは大英図書館に所蔵されている『アランデル手稿（Codex Arundel）』にあり、これはレオナルドが1480〜1518年の間に書き留めたメモをまとめたものです。
三角形の斜辺には、古イタリア語で“Equatione di Moti（運動の等価性） “と走り書きがありました。
ガーリブ氏は「レオナルドがどういう意味でこの言葉を使ったのか非常に興味を持ちました」と話します。
また、その横には壺（水差し？）から落とされる砂粒の落下軌道を描いたスケッチも見られました。
これを目にしたガーリブ氏は「重力の加速度を描こうとしたものではないか」と思い当たり、詳しく調べることにしたのです。
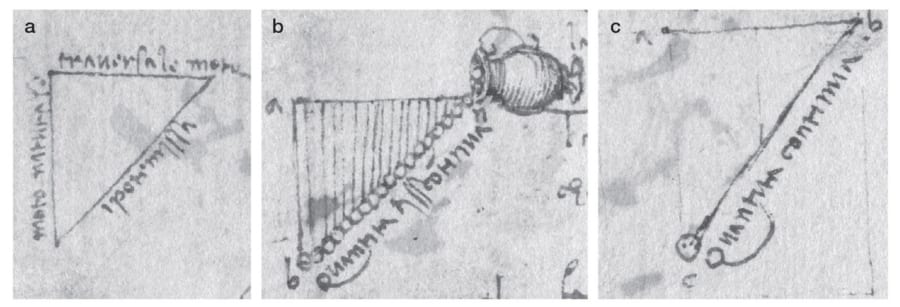
ガーリブ氏と同僚は、メモを翻訳してレオナルドの実験手法を再現し、その正確性を計算しました。
スケッチを参考に、水差しを一定の高さに設置し、そこから地面と並行に一直線上に移動させて、砂粒（代わりにパチンコ玉を使用）を流し落とす実験を再現。
このとき、水差しを同じ速度で動かすと、砂粒は地面に向かって垂直に落ちるため、スケッチのような斜線は得られません。
しかし、水差しを一定の加速度で横移動させると、砂粒は落下軌道が斜めの直線になり、スケッチにある斜線が得られるのです。
これは何をしようとした実験なのでしょうか？
ガーリブ氏は次のように説明します。
「レオナルドは『もし重力が砂粒に作用するのと同じ力で水差しを動かせば、水差しにかかる加速度は重力を模倣したことになる』と言おうとしたのだと思います。
要するに彼は、重力が一種の加速現象であることを明確に理解していたのでしょう。
そうでなければ、こんな実験をしようとは思わなかったはずです」
さらに、こちらのスケッチを見てください。
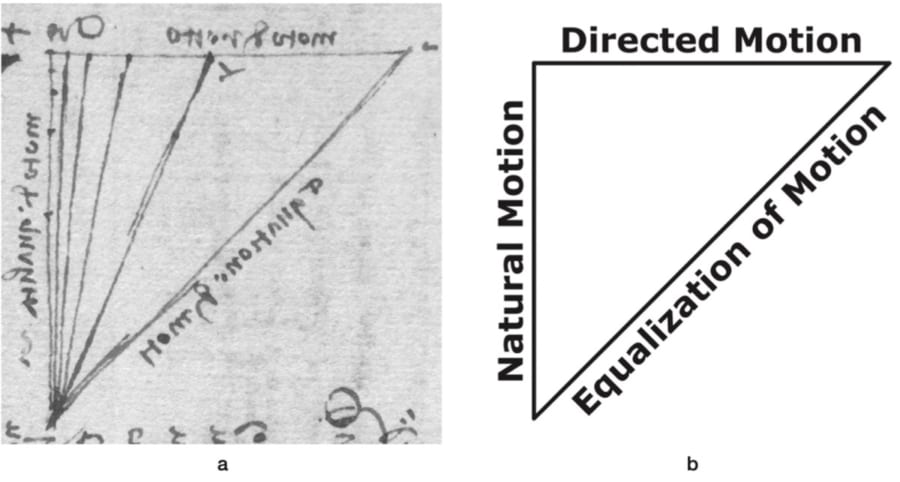
レオナルドは、2つの直交する同じ加速度場（垂直の重力によるものと水平の運動によるもの）のもとで描かれる斜辺（砂粒の落下軌道）に対して、”Equatione di Moti（運動の等価性）”という言葉を与えています。
彼は、重力が砂粒を加速するのと同じ速度で水差しを加速すれば、正三角形ができることを図示していました。
これはレオナルドが、重力による加速と、力の作用によって生じる力学的な加速が等価であることを理解していた事実を示します。
すなわち、アインシュタイン（1879〜1955）が唱えた「等価原理」と同じ法則をすでに発見していたのです。
（等価原理：重力の作用している系と加速度運動している系は同等であるという考え方）
ここで終わりではありません。
スケッチを見ると、レオナルドはさらに進んで、この加速度を数学的に表現しようとしていました。
しかしチームが彼の水差し実験をコンピューターでシミュレートした結果、これに関してはミスを犯していたことが判明しています。
彼は「自由落下する物体の落下距離は2のt乗（t＝時間）に比例する」と考えていたのです。
正しくは「物体の落下距離はtの2乗に比例する」であり、1604年にガリレオ・ガリレイが理論化しています。
現在分かっている重力の加速度は約9.8メートル毎秒毎秒であり、自由落下する物体の落下距離は、最初の1秒間で約4.9メートル、2秒間で約19.6メートルというように、重力加速度に落下時間の2乗をかけた積の半分に等しくなります。
実際、レオナルドのモデル（2のt乗）でシミュレーションを続けるとすぐに誤った答えが出ますが、最初のうち（tの値が非常に小さい）は正しいモデル（tの2乗）とよく似たグラフが導き出されました。
ガーリブ氏は「レオナルドのノートには、物体が最大4つの時間間隔で落下することしか書かれておらず、その範囲では誤ったモデルでも問題なく使うことができるのです」と話します。
現にレオナルドの描いたモデルを現代の計算に当てはめてみると、約97％の精度で重力定数（または万有引力定数：G）の値を算出していたことが明らかになりました。
驚くべきはレオナルドが、物体が落下する時間を正確に測る「時計」や、ニュートンが万有引力や運動の法則を見つけるために発明した「微積分」を使わずにここまで迫ったことです。
ガーリブ氏は、最後にこう述べています。
「レオナルドがその後も実験を重ねて、この問題をさらに深く掘り下げたかどうかは分かりません。
しかし、1500年代の初めにすでにこのような問題に取り組んでいた事実は、彼の考えがいかに時代の先を進んでいたかを示しています」
