数式で見る!指数関数的増加の凄まじさ
では、最後に
A:1から始めて2を掛けていった場合
B:0から始めて2を足していった場合
の二つの比率「B/A」を計算してみます。
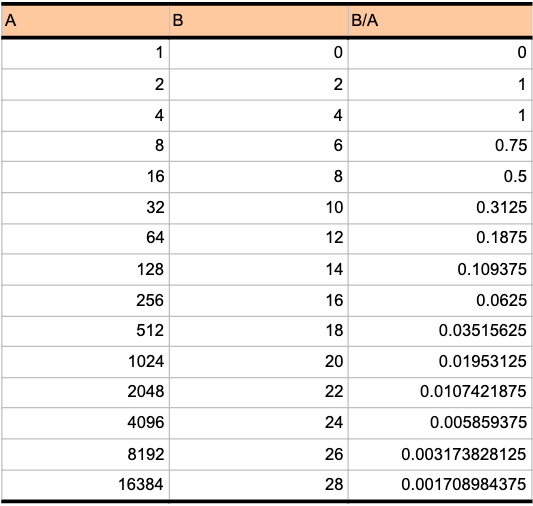
最初の0を除外すると、「B/A」は次第に小さくなり、0に近い値になっていくことがわかります。
このように、どんどんxを大きくしながら、「2x(Bのパターンに対応)」と「2のx乗(Aのパターンに対応)」の比率をとり続けていくと、限りなく0に近づくことが証明されています。このことを数式で表すと
$$\lim_{x \to \infty}\frac{2x}{2^x}=0$$
となります。
ここで注目してほしいのは、分子の一次関数「2x」も、xを大きくしていけば、どんどん大きくなる(正の無限大に発散する)関数だということです。
しかし、その増加スピードは指数関数には遠く及ばないことを、この数式は示しています。
では、この「2x」をもっと強力な関数に変えてみます。例えば、「2x」を「xの100乗」にしてみましょう。
x=3のときの「2のx乗(指数関数)」は
$$2^3=8$$
となります。
一方、x=3のときの「xの100乗」は
$$3^{100}=515377520732011331036461129765621272702107522001$$
となります。これなら、余裕で指数関数に勝てそうですね!
では、xを限りなく大きくしてみましょう。すると…
$$\lim_{x \to \infty}\frac{x^{100}}{2^x}=0$$
となってしまうのです!「100乗」にしても、結局は指数関数が圧倒的大差で勝ってしまうんですね…。
実は、この「xの100乗」を、さらに大きな「xの2億乗」や「xの5000京乗」などにしたとしても、同じことが起こり、結局は0に限りなく近づいてしまいます。
直感的には信じにくいことですが、それほどまでに指数関数の威力は凄まじいのです。
このように、「指数関数的増加」は、もはや私たちの感覚では捉えきれないほど、猛烈なスピードで加速しながら増えていきます。
しかし、最初の時点では、増え方は比較的ゆっくりとしているので、秀吉のように私たちは油断してしまうのです。
「最初は弱そうに見えたのに、実は超強キャラだった!」という、バトルマンガのキャラクターのような指数関数。実に恐ろしいですね。
今回紹介した内容のほとんどは、高校数学の現行課程で学ぶことができます。しっかり勉強しておくと、新型コロナ対策の専門家の発言をよく理解できるようになるかもしれません!





























![よーく聞いてね!3つのヒントで学ぶ!どうぶつカード ([バラエティ])](https://m.media-amazon.com/images/I/51zT3OcliFL._SL500_.jpg)
![シルバーバック かわいい海の生きもの CUBE 2X2 キューブ ツーバイツー|海の生き物デザイン 立体パズル スピードキューブ 5cm 子ども〜大人向け 知育 ギフトに最適 ([バラエティ])](https://m.media-amazon.com/images/I/41EJOOLgGXL._SL500_.jpg)