グラフで見る!指数関数的増加の凄まじさ
では、この「指数関数的増加」を実際にxy-座標平面上のグラフで見てみましょう。
比較のために、指数関数(先ほどのAのパターンに対応)
$$y=2^x$$
と一次関数(先ほどのBのパターンに対応)
$$y=2x$$
の両方のグラフを描いてみます。すると…
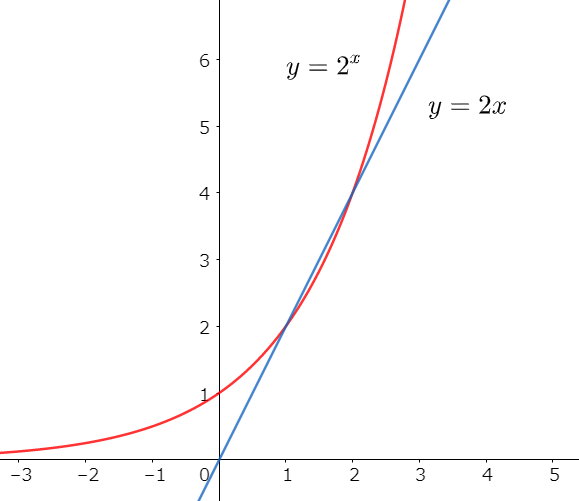
確かに、赤い線の指数関数「2のx乗」の方が、青い線の一次関数「2x」よりも大きくなっていきそうではあります。しかし、その威力はイマイチ見えてきません。
では、縮尺を変えて、もう少し広い視野でグラフを見てみると…
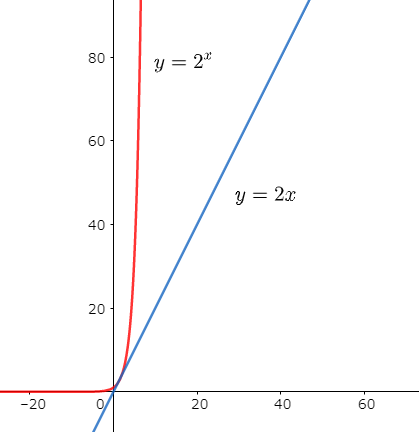
肉眼では「もはや直角じゃないか!?」と思ってしまう程に、指数関数「2のx乗」は一気に増えていることがわかります。直線である一次関数「2x」とは対照的です。
これには、実は「微分」が関わっています。
一次関数「2x」を微分すると、2という定数になります。これは、一次関数「2x」は一定の速度で増えていくことを表しています。
一方、指数関数「2のx乗」を微分すると…
$$2^x \log{2}$$
となります。注目してほしいのは、微分しても「2のx乗」が残っている点です。
これは、指数関数「2のx乗」の増加率もまた、指数関数的に増加することを表しています。
つまり、指数関数は猛烈にガンガン加速して増えていくのです。
おまけとして、一次関数「2x」よりも、大きくなりやすい二次関数「xの2乗」を採用して、指数関数「2のx乗」と比べてみます。
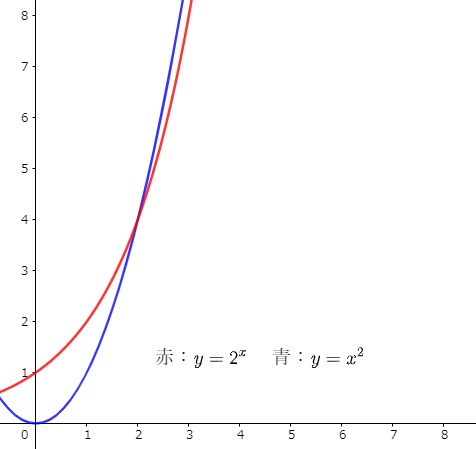
赤い線の指数関数「2のx乗」が、青い線の二次関数「xの2乗」に負けています!
ついに指数関数にも負けが訪れたか…と思いつつ、グラフの縮尺を変えてみると…
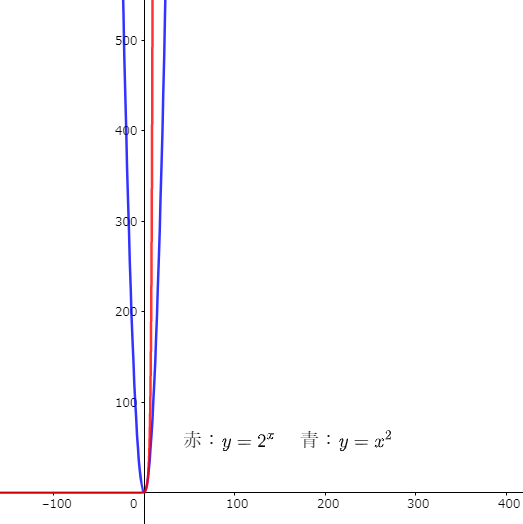
さすが指数関数!二次関数にも、しっかり勝利していたのでした。





























![よーく聞いてね!3つのヒントで学ぶ!どうぶつカード ([バラエティ])](https://m.media-amazon.com/images/I/51zT3OcliFL._SL500_.jpg)
![シルバーバック かわいい海の生きもの CUBE 2X2 キューブ ツーバイツー|海の生き物デザイン 立体パズル スピードキューブ 5cm 子ども〜大人向け 知育 ギフトに最適 ([バラエティ])](https://m.media-amazon.com/images/I/41EJOOLgGXL._SL500_.jpg)