相関係数をビジュアルで実感しよう!
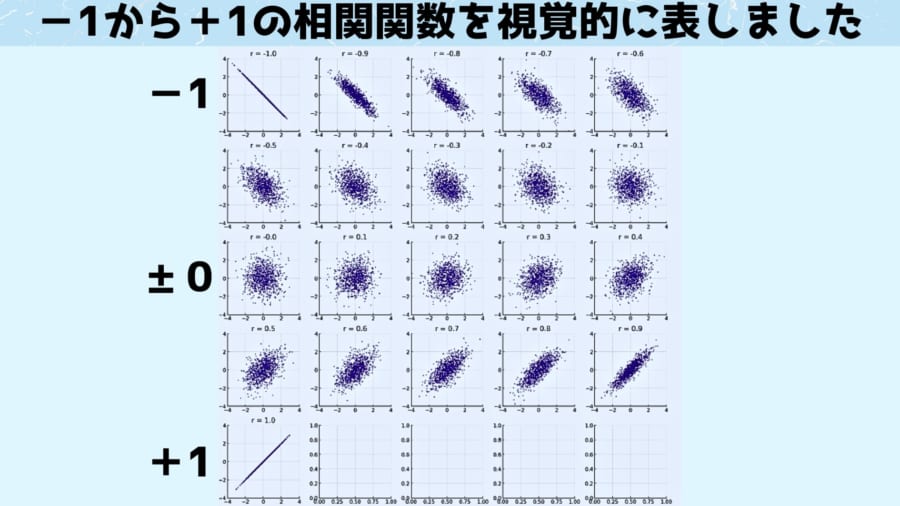
相関関係とは2つのデータの間にある関連性を指す言葉です。
そしてその相関関係の強さを表すのが、相関係数です。
そんなさまざまな現象の相関係数について語る前に、まずは相関係数というものを視覚的に確認してみましょう。
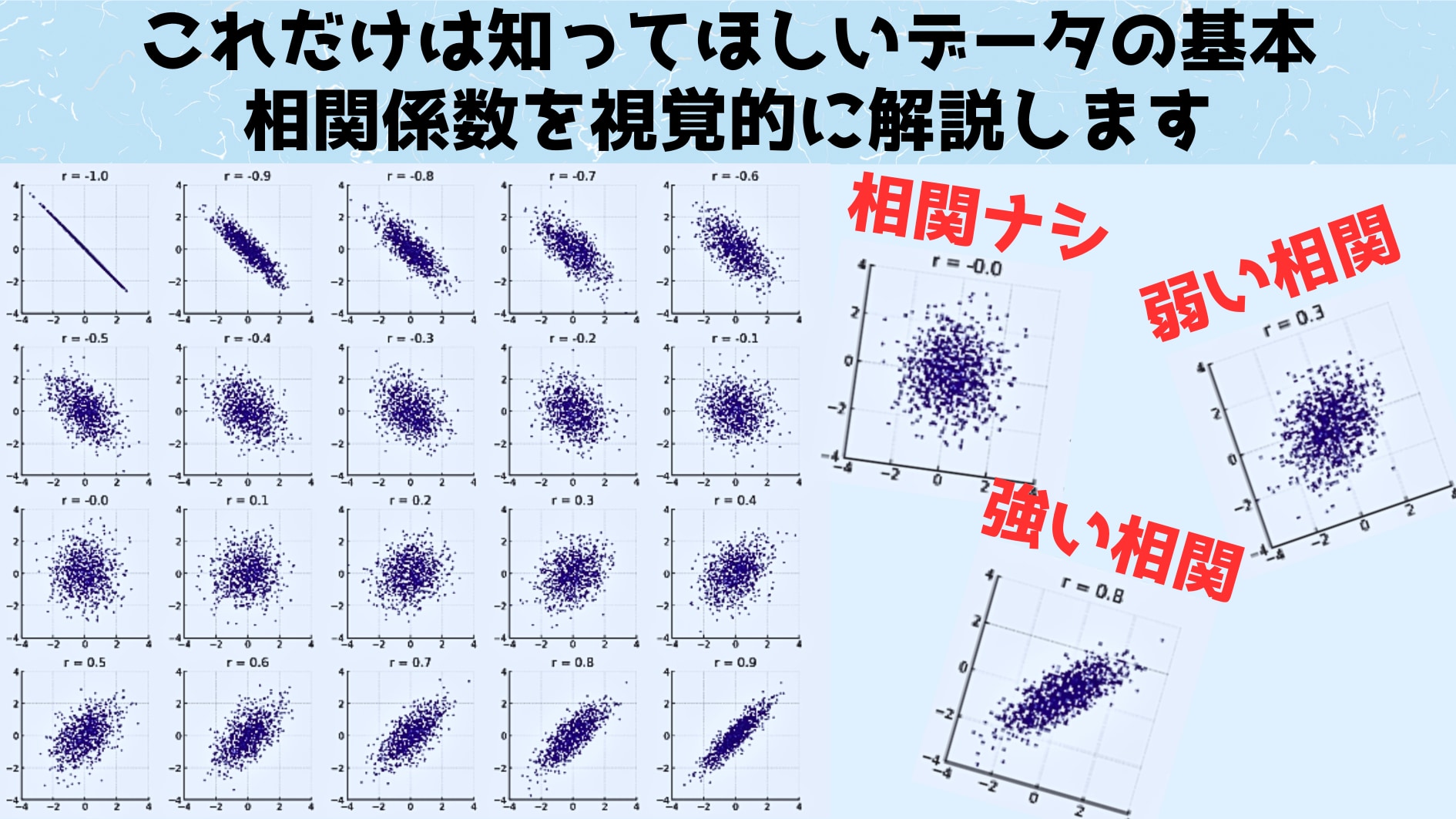
上の図は相関係数を、おおよそ0.1刻みで表示したものとなっており、相関係数が「-1(完全に逆相関)」から「1(完全に相関)」までが並べられています。
相関係数0の場合
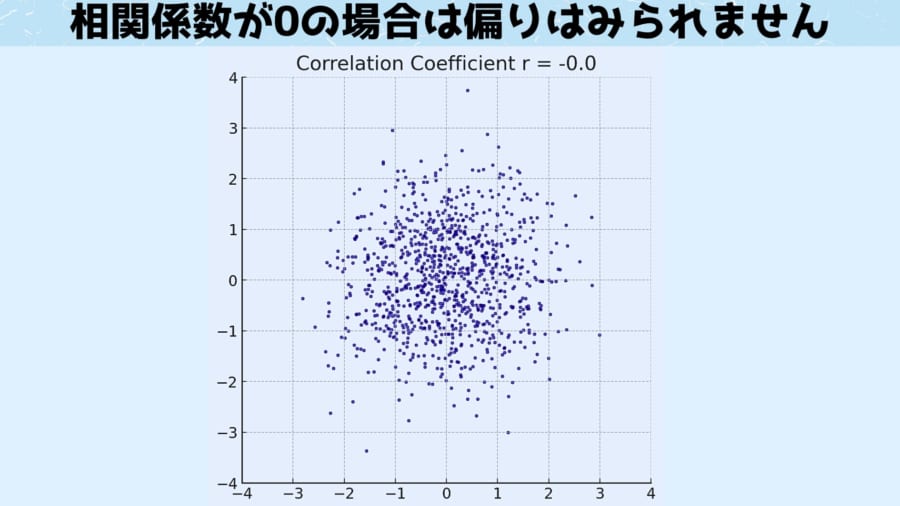
グラフをみれば、相関係数0のグラフは中央に団子状に固まっており、横軸や縦軸の数値変化に対して、特定の「傾き」を見せることはありません。
たとえるならば、今日の朝ごはんのメニューの種類数とここ100年の間で観察された超新星爆発の頻度との関連性などが当てはまるでしょう。
自分の朝ごはんが超新星爆発に関連している人がいないかぎり、ポイントの集団に傾きがうまれることはありません。
相関係数1の場合
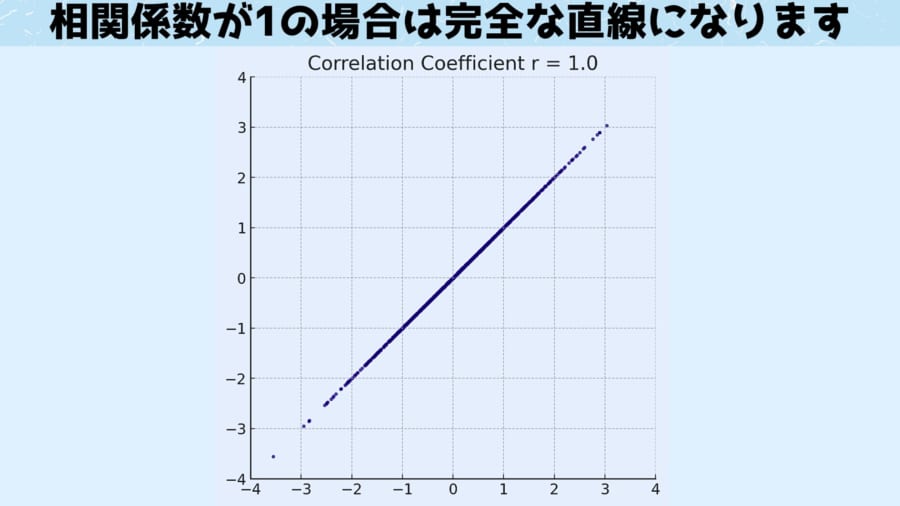
一方、相関係数が1のグラフは全てのポイントが直線状に整列しており、「横軸の値が○○ならば縦軸の値は絶対に✕✕になる」という完璧な比例が成立していることがわかります。
ただ現実問題として、2つの現象が完璧に相関することはなく、現実世界で相関係数が「1」に達する事例はほぼ存在しないと考えられます。
(※相関係数が1の場合、例外が全く存在しないことを示しているからです)
特にさまざまな要因が関係する社会学や心理学の分野において、相関係数が0.9以上になることは極めて稀となっています。
「絶対は存在しない」という言葉も、現実世界で相関係数1の現象がないことから言われているのでしょう。
ここまでは、誰もが納得する内容だと思います。
ビジュアル的にも団子と直線という明確な差が見て取れるからです。
では弱い相関に該当する、相関係数「0.1」や「0.2」はどうでしょうか?






























![よーく聞いてね!3つのヒントで学ぶ!どうぶつカード ([バラエティ])](https://m.media-amazon.com/images/I/51zT3OcliFL._SL500_.jpg)