最初の選択と途中変更では選択している扉の数が違う
この問題で見落としてはならない重要な点は、これがモンティ氏の仕掛ける心理作戦ではないということです。
もし、正解を知っているモンティ氏が最初にプレイヤーの選んだ扉によって、ハズレの扉を開いて選択変更を提案するかどうか選べるなら、これはモンティがプレイヤーを揺さぶるための作戦になり、容易に答えの出ない問題になるでしょう。
しかし、このゲームではモンティ氏は必ず最初の選択後、残った扉からハズレを1つ間引きして、プレイヤーに選択変更の機会を提案するルールになっています。
この条件を踏まえた上で考えると、このゲームは次のような状況になります。
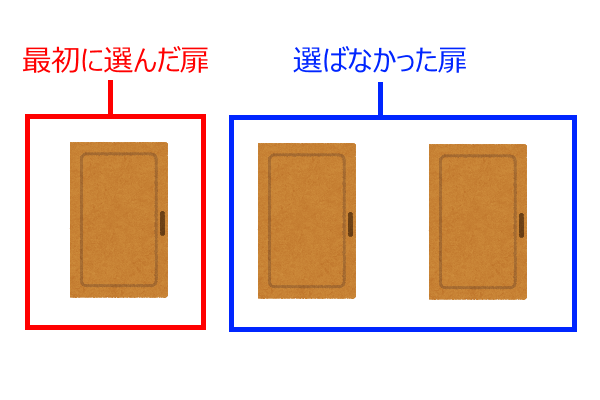
モンティは選ばなかった扉のうちハズレの方を開いてもう一度選び直してもいいと提案します。それはつまり次のような状況です。
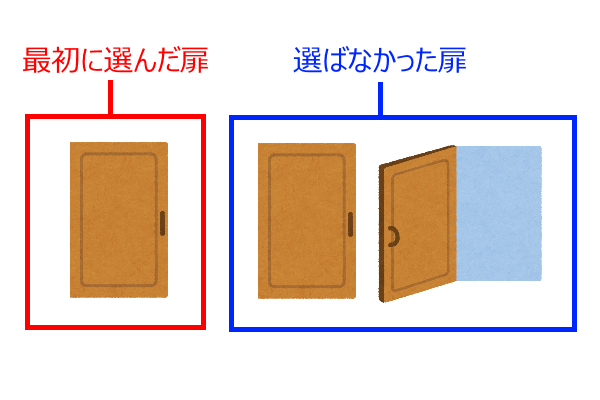
この状況を見るとわかると思いますが、ハズレの扉を明かした上で選択を変更するということは、1度のゲームで2枚の扉を選んでいることに等しいのです。
しかし、多くの人は直感的にこの状況を次のように勘違いして、確率は2分の1だと考えてしまいます。
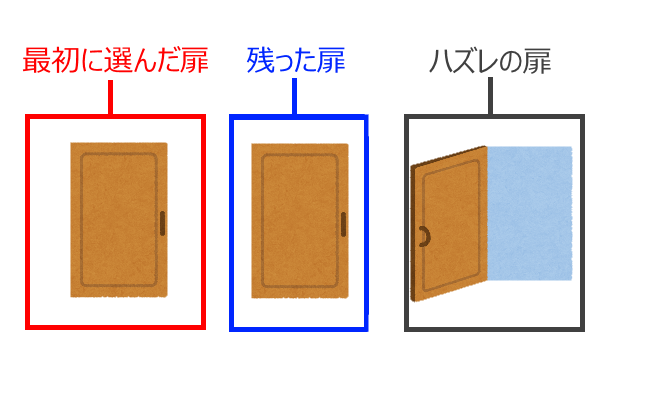
もし最初に扉を選択せずにモンティ氏がハズレの扉を明かしたとしたら、上のイラストのような2択状況になり扉の正解確率は2分の1になります。
しかし、最初に1つ扉を選んでいるというのがミソになります。
どちらでも同じことでしょ？ と思ってしまう人はモンティ氏がプレイヤーの選んだ扉を除外してハズレの扉を開いていることに注意しましょう。
それがこの問題のいちばん重要な点です。残された扉は常に2つ1組のセットになっているのです。
