「数学」が進化の法則を制御していたと判明！
数論は純粋に数の性質のみを扱う分野であり、数学者以外には理解し難いストイックな分野とされています。
たとえば素数の出現パターンを解明するのも数論の分野となっています。
こうしたただの数の性質を論じているだけの分野でありながら、不思議なことに数論に関わる法則は、自然界のさまざまな場所に見ることが出来ます。
動物や植物の形態は実に多様で、そこには「堅苦しい」数学が入り込むスキがないように思えてきます。
しかし松ぼっくりのカサ、シダの葉、ヒマワリの種などの配列パターンを詳しく調べてみると、そこには数学をもとにした規則性が存在することが知られています。
特に有名なのは左右を「1」で囲まれたピラミッド型をした「フィボナッチ数列」や「フラクタル」と呼ばれる数学的概念であり、数論を構成します。
そして今回オックスフォード大学の研究者たちは、生命進化と数論の関係に注目しました。
進化と数論の関係が解明されれば、生命の中にパターンが数論と関連する謎の解明にもつながるかもしれません。
そこで着目されたのが、進化の原動力となる突然変異でした。
突然変異は遺伝病など目に見える変化を起こす場合もありますが、変異が起きた場所によっては影響力が低く、生物の外観や行動に目だった変化を起こさない場合もあります。
このような目立った変化を起こさない変異は「中立」突然変異と呼ばれています。
また中立突然変異は時間の経過とともに一定の速度でDNAに蓄積していくことが知られており、中立突然変異が起きた量を比べることで、異なる種が共通の先祖から枝分かれしたタイミングを知ることが可能になります。
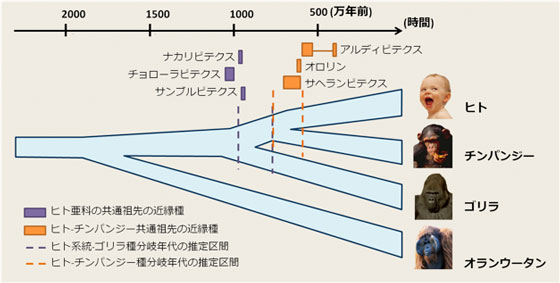
近年、ウイルスや耐性菌の流行などで、生物の進化のしやすさは強みにみえるでしょう。
ただ進化は早すぎても害になります。
進化の速度が速すぎると、変異によって誕生した優秀な能力を持つ子孫が「繁栄する前に」新たな突然変異が起きてしまい、結果として生存に不利に働いてしまいます。
そのため生物は、突然変異に対する防御力（以下、堅牢性と表記）を備えています。
この堅牢性を言い換えれば、起きた変異が中立突然変異になる確率となるでしょう。
たとえば、ある遺伝子の分析では、遺伝子配列の3分の2にあたる部分はランダムな変異が起きても問題ない領域であることがわかりました。
この結果は、突然変異の66%が中立突然変異であり、生物に目だった変化を起こさないことを示しています。
生物たちは変異に対する堅牢性を高めることで、種としての体面を保ち、子孫たちが無秩序な姿になるのを防いでいたのです。
ただ現在のところ、この堅牢性がどの程度で、最大値のようなものが存在するのかは不明でした。
そこで研究者たちは特定の遺伝子から作られるタンパク質と低分子RNAを対象に、最大でどれくらいの変異を、目立った変化なしに蓄積できるかを数学的に分析することにしました。
すると非常に興味深い結果が得られました。
堅牢性の最大値は「目立った影響をおよぼす変異の割合（中立突然変異でない割合）」の対数（log）に比例するという、極めて簡素な数式で描けることが判明したのです。
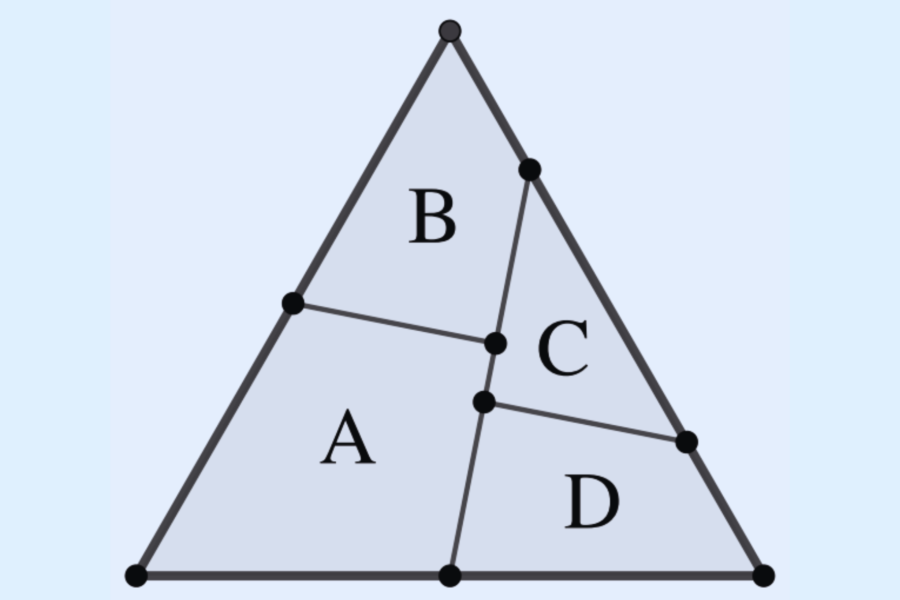
また「堅牢性の最大値がフラクタルな特性を持つ」ことが判明します。
フラクタルとは上の図のように「部分の構造」と「全体の構造」が同じであり、どれだけ大きくなっても全体のパターンが変わらない特性をもつものです。
生物の場合では、ロマネスコの一部をとってそれを拡大してみても、ロマネスコ全体と同じような形を持っていることがわかります。
「堅牢性の最大値がフラクタルな特性を持つ」というのは、細胞内の小さな領域から体全体に至るどのスケールで見ても、堅牢性の最大値が同じ数式で表記できることを示します。
小さな領域と大きな領域では関わる数式が別物だと思われていましたが、生物の突然変異に抵抗する堅牢性は、どの倍率レンズを使って観察しても、同じだったわけです。
単一の数式により生物の進化法則の一部が理解できるという結果は、進化が数論的な現象であることを示します。
数論は宇宙の構造だけでなく生物の体のパターンや進化法則も支配する、究極の法なのかもしれません。
