時空はより高度な概念の投影に過ぎない：コスモヘドラで時空は消える (2/3)

時空の全てを多面体の物語に変換する

もともと散乱振幅を表すアッソシアヘドロンは「粒子間の運動量をパズルのピースのようにつなげていくと、多角形や多面体が自然にできあがる」というアイデアから始まりました。

時空をベースに作られた大量の方程式には目をつぶり、運動量だけに着目してそれを矢印として描き続けていると、それらを繋ぐポリゴン（多角形）が出現したのです。

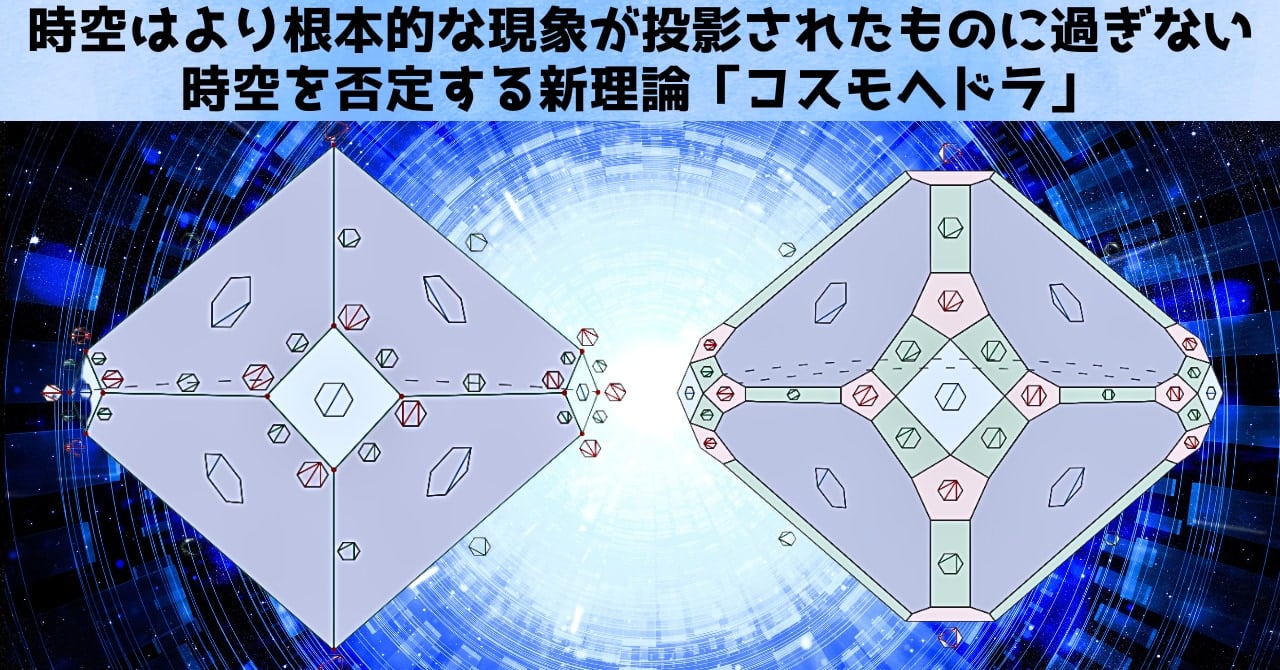
コスモヘドラは、このアッソシアヘドロンに“余分な面やパラメータ”を加えて拡張し、より複雑な「宝石」のような立体にまとめたものです。

イメージとしては「アッソシアヘドロンの各辺を少し“削る（Shave）”ことで、新たな面を追加する」という感じになります。

すると、その形がぐんと複雑になり、その分「宇宙の波動関数」のような巨大な系まで一度に扱えるようになるのです。

波動関数は物体を波として記述するときに現れるもので、たとえば電子を1つの波として扱う場合には「電子の波動関数」を用います。

また電子や分子などの多数の粒子からなる物体を扱う時にも、波動関数でその物体の波としての性質を現わすことが可能です。

この範囲には理論的に限りがなく、電子だけでなく、原子、ウイルス、そして人間といった巨大な系にいたるまで、厳密にいえば波動関数を用いて記述可能と考えられています。

したがって、究極的には”宇宙全体をひとつの波”として扱うことも理論上は不可能ではないわけです。

多面体を複雑にしただけで「宇宙の波動関数」のような大それた系まで扱えるようになるというのは信じがたいでしょう。

しかし、理論的には、運動量や因数分解に関する幾何学的なルールを拡張し続けることで、複雑さをさらに高め、ついには全宇宙をも波として記述する試みが視野に入るのです。

実際にそこまで到達できるかは今後の研究次第ですが、少なくとも「数学的・理論的には道が開かれている」という点が、この幾何学的アプローチの魅力といえます。

もしこの試みが上手くいって「宇宙の波動関数」を内包する輝かしい多面体を生み出せるとしたら、それはいったいどんな姿をしているのか？

まだその答えは得られていませんが、宇宙の全てを内包する宝石のような多面体を見たいという人は決して少なくないはずです。