ブラックホールを素粒子と考えると弦理論が見えてくる
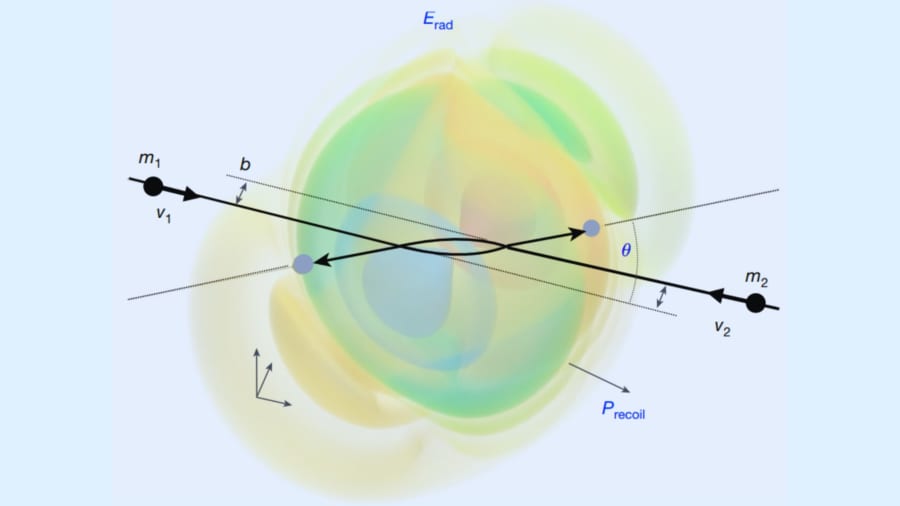
では、研究チームはどのようにしてブラックホール散乱から弦理論由来の数学構造を見いだす方法を発見したのでしょうか？
鍵となったのは、素粒子物理で培われた散乱計算の手法をブラックホール研究に応用するというアイデアです。
ブラックホールは十分遠くから見れば大きさを無視して一点状の粒子として扱えるため、ミクロな粒子散乱のFeynman積分をマクロな重力散乱に移植できるのです。
具体的には、二体問題における重力相互作用を摂動論で近似展開し、段階的に精度を上げながら解析しました。
今回の論文では、その精度をこれまでになく高い第五次ポスト・ミンコフスキー近似（5PM）まで引き上げています。
この高次計算により、ブラックホール散乱角、放出される重力波エネルギー、そしてブラックホールの反動速度といった量を前例のない精度で導出することに成功しました。
主なポイントは次の三点です。
第一に、散乱角とは、ブラックホール同士が接近してから遠ざかるまでの過程で進行方向が重力によって何度曲げられたかを示す角度です。
第二に、重力波放出エネルギーは、すれ違いざまに放射された重力波が運ぶ総エネルギーを表します。
第三に、ブラックホールの反動速度は、放出された重力波に対する反作用としてブラックホールが蹴り飛ばされる運動量を速度として表したものです。
5PMというかつてない高次近似を実現するため、研究チームはスーパーコンピューターによる大規模計算を行いました。
問題を線形方程式の形に再構成し、数百万に及ぶFeynman積分を効率よく処理することで、三十万コア時間にも達する大規模計算を成し遂げています。
研究チームをさらに驚かせたのは、そうして得られた解の中に現れた意外な数学的パターンでした。
計算精度を引き上げるほど、カラビ・ヤウ多様体（複素3次元＝実6次元）に関連する特殊な関数がエネルギー放出の解に自然と組み込まれることが分かったのです。
これらは本来、弦理論や代数幾何の文脈で抽象的に研究されてきたもので、今回の結果により現実の天体物理現象を高精度で記述するうえで欠かせない存在だと示されました。
近似の精度が低い計算では現れない幾何学的構造が、ブラックホール散乱の重力波エネルギーを正しく予測する際には必要不可欠だという点は、一般相対性理論と高度な数学の間に新たな橋をかけるものといえます。
数学では、ある関数の背後に特定の幾何学的図形が対応するケースが多々あります。
たとえば三角関数は円の幾何学と深く結びつき、楕円関数はトーラス（ドーナツ状の曲面）に対応します。
今回浮上したカラビ・ヤウ多様体は複素3次元版のトーラスをさらに複雑にしたような構造で、今回の計算に登場した特殊関数は、まさにその多様体の周期積分と密接に関係しています。
さらに研究チームは、得られた散乱角の精度を確かめるため、数値相対論シミュレーションと比較を行いました。
ブラックホール間の衝突パラメータが大きい（すなわち遠距離でのすれ違い）ケースでは、高次摂動計算の結果とシミュレーションがほぼ一致することが示されています。
一方、正面衝突に近いほど接近するケースでは双方の結果が食い違い始め、そうした領域ではさらなる摂動展開の高次化や数値計算の併用が今後の課題とされています。
