↓↓動画でも解説しています。
地球の大きさを測定したエラトステネス
古代の人たちは、地球が亀や象の背に乗った平坦な地面だと考えていた…わけではありません。
そんな考えの人もいたかもしれませんが、紀元前のギリシャ人はすでに地球が丸い球であることを理解していました。
このことは月食でできる地球の影が丸いことや、水平線の向こうから船がやって来る時、まずマストの上部が見え、それから徐々に船体が見えてくるという事実から明らかでした。
この事実を聞いた子供たちを悩ませる「南半球の人はなぜ落ちないの?」という疑問も、ギリシャ人たちはクリアしていました。
彼らは「すべてのものは宇宙の中心に向かって引かれており、地球は宇宙の中心にある」と考えていたのです。
では地球が球だとして、それは一体どのくらいの大きさなのでしょう?
このことを最初に明らかにしたのが、当時の世界最高学府だったアレクサンドリア図書館の館長エラトステネスでした。

あるときエラトステネスは、エジプト南部シエネの街に「夏至の日の正午になると、底まで明るく太陽で照らされる井戸がある」という話しを耳にします。
彼はこの話から、夏至の正午に太陽はちょうどシエネの井戸の真上に来るのだと考えました。
しかし、シエネから数百km離れたアレクサンドリアでは、決してそんなことは起こりません。
シエネとアレクサンドリアで、同時に太陽が真上に来ないのは地球が球形をしているためだと気づいたエラトステネスは、これを利用して地球の大きさを測ることができないかと考えたのです。
そこで彼は夏至の正午に、アレクサンドリアに棒を立てその影の長さから、アレクサンドリアに差す太陽光の角度を測定しました。
この太陽光の角度は、シエネとアレクサンドリアから地球中心にまっすぐ線を引いたときの角度と同じになります。
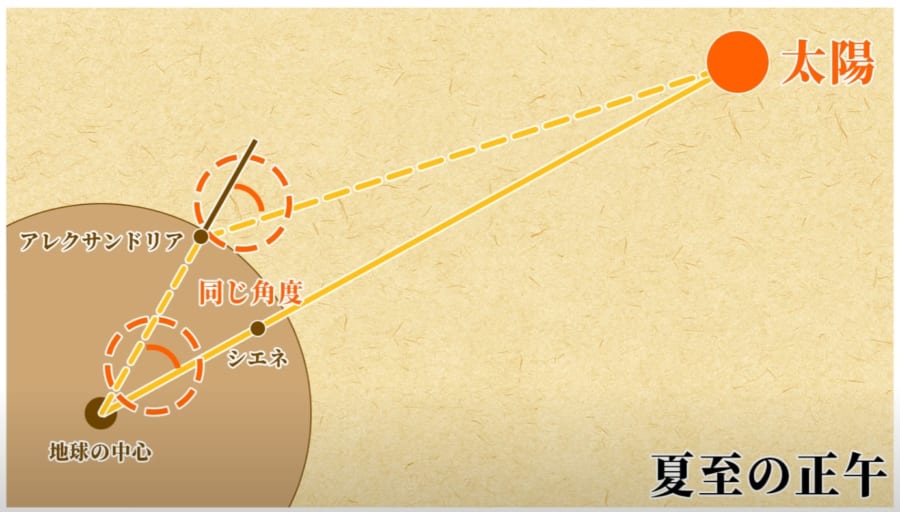
上の図で見ると分かるように、この事実の重要な点は、
【シエネとアレクサンドリアの距離:地球一周の距離 = アレクサンドリアの太陽光の角度:360度】
という関係で一致することです。
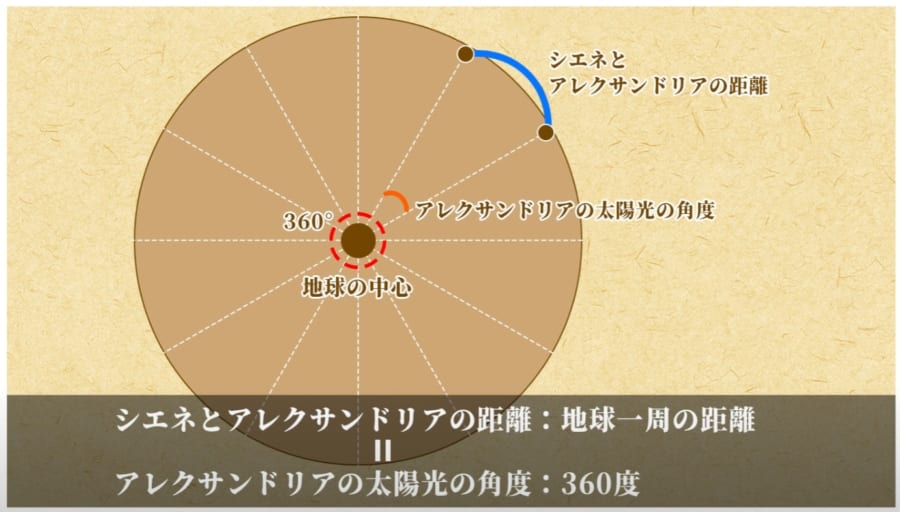
つまり、夏至の正午にアレクサンドリアで測った太陽の角度を360度で割れば、シエネからアレクサンドリアまでの距離が地球一周の何%にあたるかを計算することができるのです。
エラトステネシスはこの方法によって、地球を一周した距離が25万スタディオンだと導きました。
スタディオンという単位が、正確にどの程度の距離を表すものだったのかは残念ながら現代には伝わっていません。
しかし、オリンピュアの徒競走で使われる標準的な距離だったという情報から、当時の競技場のサイズを参考に推測すると、エラトステネスの導いた地球の距離は、実際の値から大きくとも15%しかずれていなかった可能性があります。
いずれにせよ重要なのは、たった1本の棒と優れた人間の頭脳によって、紀元前の人々は地球という惑星のおおよそのサイズを知っていたということです。
そして、地球のサイズが分かったことで、彼らは月や太陽についても、その大きさや距離を計算できるようになるのです。




























![[W.P.S.] 防水スプレー 除菌 抗菌 防汚 機能付き 大容量420ml 日本製](https://m.media-amazon.com/images/I/41aHfy9uuZL._SL500_.jpg)
![[WILL CLENS] シューズパウダー 日本製 無香料 シューケアキット 靴 消臭 パウダー (1本)](https://m.media-amazon.com/images/I/41m8Ig2XigL._SL500_.jpg)
![よーく聞いてね!3つのヒントで学ぶ!どうぶつカード ([バラエティ])](https://m.media-amazon.com/images/I/51zT3OcliFL._SL500_.jpg)