太陽までの距離は紀元前に測定されていた! 必要なのは1本の棒と偉大な頭脳 (3/3)

月を利用した太陽の測定

宇宙の神秘に近づくために、まず人類に必要だったことは、太陽や月が神の化身ではなく、宇宙に浮かぶ天体であると理解することでした。

このことを最初に主張したのは、紀元前400年代の哲学者アナクサゴラスです。

アナクサゴラスは、太陽を神などではなく白く熱い岩石であると主張しました。夜空の星も同様の熱い岩石だが、こちらは非常に遠くにあるので太陽のようには感じられないのだと言ったのです。

さらに月は冷たい岩石であり、太陽の光を反射しているだけだと論じました。

彼の住んでいたアテナイは、かなり学問に寛容な都市でしたが、さすがに太陽や月を神ではなく岩石だ、と主張したことには反発が多く、残念なことに彼は街を離れることになってしまいます。

そんなアナクサゴラスの考えを後に発展させたのが、さきほど月の大きさの測り方でも登場したアリスタルコスです。

アリスタルコスはアナクサゴラスの考える通り、月が太陽光を反射しているなら、半月のとき月と太陽と地球は直角三角形を描いているはずだと考えました。

もしそうなら、地球と太陽の作る角度がわかれば、三角法によって月と地球の距離と地球と太陽の距離の比を明らかにすることができます。

アリスタルコスが実際に半月のとき、太陽と地球が作る角度を測定したところ、それは87°でした。このことからアリスタルコスは、太陽までの距離は、月までの距離のおよそ20倍だと導きました。

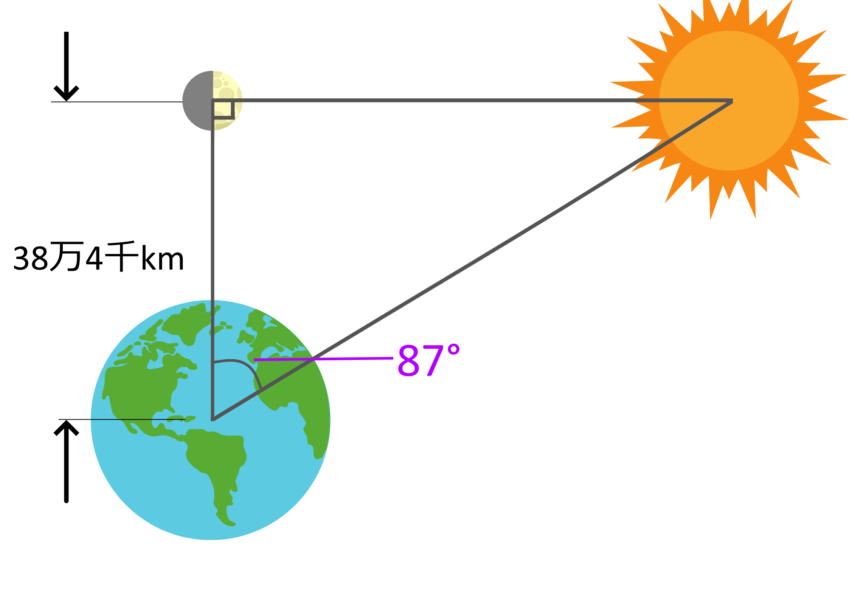
実際は、現代の技術で調べると、この角度は正確には89.85°であることがわかっており、太陽までの距離は月までの距離のおよそ400倍です。

アリスタルコスは、この角度を調べるためにかなりの苦労をしたでしょうが、技術的な精度の限界で正しい値を知ることはできませんでした。

しかし考え方は間違っておらず、ズレがあるものの彼は地球と太陽の距離を推定することができたのです。

では、最後に太陽の大きさはどれほどなのでしょう？

この測定方法はすでに解説しています。

日食のとき、月は太陽をすっぽりと覆い隠してしまいます。このことからアリスタルコスは、地球から見た月と太陽の大きさがほぼ同じであることを知っていました。

だとすれば、さきほど爪と月を使って比を取った方法を、今度は月と太陽で行えばいいのです。

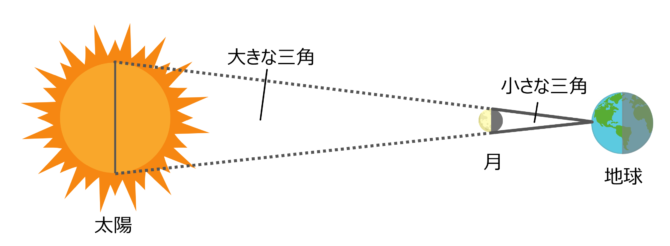
月の大きさと、月までの距離、太陽までの距離はわかっているのですから、

【太陽の大きさ：月の大きさ　＝　太陽までの距離：月までの距離】

という関係を利用して、おおよその太陽までの距離を知ることができるのです。

こうして、紀元前の昔、古代ギリシャの人々はおおよその太陽までの距離やその大きさまでを計算して知っていました。

現代はさまざまなテクノロジーの進歩によって、複雑な問題を高い精度で調べることができ、私たちは世界中のさまざまな発見を素早く知ることができます。

しかし、1本の棒と優れた頭脳と鋭い観察眼だけで、はるか2000年以上の昔、人類はこれだけの事実を明らかにしていたのです。

こんな話を聞くと、現代の私たちは本当に自分の頭脳を最大限に活かしきれているのかな、と考えさせられてしまいます。