月を測るのは月食と爪
月の大きさを推測する方法は、エラトステネスより以前にアリスタルコスという古代ギリシャの哲学者が考えついていました。
このときアリスタルコスが利用したのが、月が地球の影に隠れてしまう現象「月食」でした。
太陽は月と地球の距離よりもずっと離れたところにあるはずです。そのため月にかかる地球の影は、地球とほぼ同じ大きさだと推測することができます。
月食の時、月が地球の影の真ん中を通っていると仮定すると、月の端が地球の影にかかり始めてから、完全に隠れて消えるまでの時間は月の直径の目安になります。これは50分でした。
そして月が地球の影に入ってから、端が影の外に出てくるまでにかかる時間は地球の直径の目安になります。こちらは200分でした。
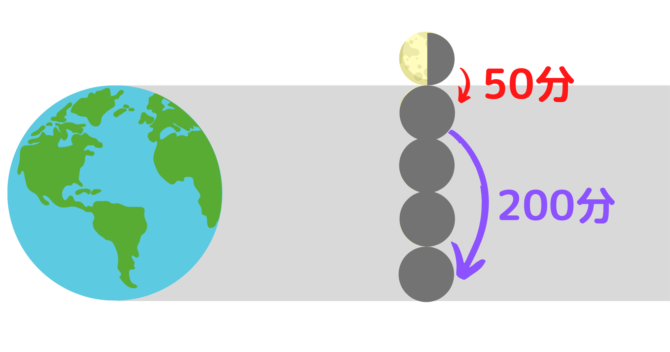
月が完全に隠れるまでに50分、そして地球の影から抜け出すまでに200分かかったということは、月の大きさは地球の約4分の1だと推測することができるのです。
ただアリスタルコスは、この事実に気づいても地球のサイズがわからなかったため、月の大きさを計算することができませんでした。
しかし、エラトステネスは地球一周が25万スタディオンということを発見したので月のサイズも計算することができたのです。
いつまでも謎のスタディオンではわかりにくいので、現代の単位4万キロメートルに直して考えていきましょう。
地球の直径は、外周の「4万キロメートル」をπで割ればいいので「1万2700キロメートル」です。月の直径はその4分の1なので「3200キロメートル」となります。
月の大きさはわかりましたが、果たして月と地球の距離はどうやって求めればいいのでしょうか？ これは月の大きささえ分かれば簡単に求めることができます。
満月の夜に、月に向かって腕を伸ばし、人差し指を立てると指先の爪がすっぽりと月を隠してしまいます。このとき指先の爪と、月の大きさはほぼ同じに見えることになります。
これは、爪の大きさと腕の長さの比が、月の大きさと月までの距離の比に等しくなっていると考えることができるのです。
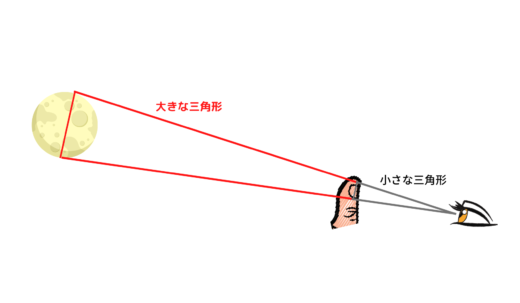
実際はもう少しきちんとした道具を使用して測ったでしょうが、エラトステネスがこうした方法で比率を計算したところ、月までの距離は月の大きさのだいたい120倍だろうと検討がつけられました。
つまり月の直径の120倍、約38万4千キロメートルが地球から月までの距離だとわかったのです。
では、月よりもはるかに遠く、はるかに巨大な太陽を古代ギリシャ人はいかにして測定したのでしょうか？
