フェルマーの小定理とは?
まずは、フェルマーの小定理がどんな定理か見てみましょう。
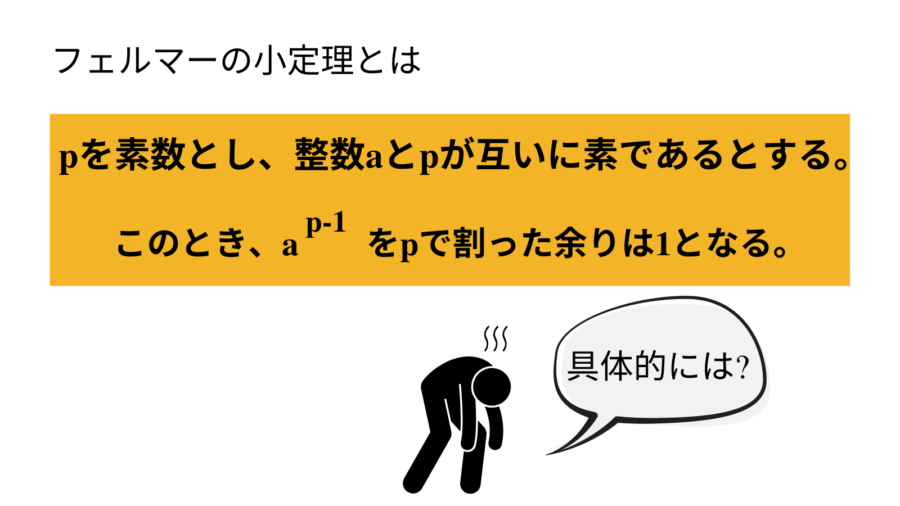
【フェルマーの小定理】
pを素数とし、整数aとpが互いに素であるとする。このとき、ap-1をpで割った余りは1となる。
(※「素数」とは、1より大きい整数で、1と自分自身以外に正の約数を持たない数のことです。例えば、2や3や5は素数ですが、6は2と3を約数に持つので素数ではありません)
(※「aとpが互いに素」とは、「aとpの最大公約数は1」という意味です。例えば、3と20は互いに素ですが、24と36は、最大公約数が12なので互いに素ではありません)
こう見ると少し難しそうですが、具体例を考えてみるとわかりやすいですよ。
p=5の場合を試してみましょう。
5(pに対応)と互いに素な整数「2,3,4」(aに対応)について、フェルマーの小定理を確認してみます。
それぞれの数を(p-1)乗すれば良いので、今回のケースでは、(5-1)乗、つまり、4乗していきます。
最初に、2を4乗してみると、
$$2^{4}=16$$
となります。
16は5で割ると1余りますね(商3余り1)。
次に、3を4乗してみると、
$$3^{4}=81$$
となります。
81も5で割ると1余りますね(商16余り1)。
最後に、4を4乗してみると、
$$4^{4}=256$$
となります。
256も5で割ると1余りますね(商51余り1)。
「5と互いに素な整数」を4乗して、5で割ると、必ず余りが1となるのです!

今度は、p=7の場合を試してみましょう。
7(pに対応)と互いに素な整数「5,6」(aに対応)について、フェルマーの小定理を確認してみます。
それぞれの数を(p-1)乗すれば良いので、今回のケースでは、(7-1)乗、つまり、6乗していきます。
まずは、5を6乗してみると、
$$5^{6}=15625$$
となります。
15625は7で割ると1余ります(商2232余り1)。
次に、6を6乗してみると、
$$6^{6}=46656$$
となります。
46656は7で割ると1余ります(商6665余り1)。
7の場合についても、「7と互いに素な整数」を6乗して、7で割ると、必ず余りが1となるのです!
フェルマーの小定理は、5や7だけでなく、「どんな素数pについても、『pと互いに素な整数』を(p-1)乗して、pで割ると、必ず余りが1になる」ということを主張しています。
シンプルながらも、数学の不思議さを感じられる定理ですね。
ぜひ、p=5や7以外についても計算してみてはいかかでしょう。フェルマーの小定理の不思議さを、さらに実感できるはずです!































![[W.P.S.] 防水スプレー 除菌 抗菌 防汚 機能付き 大容量420ml 日本製](https://m.media-amazon.com/images/I/41aHfy9uuZL._SL500_.jpg)
![[WILL CLENS] シューズパウダー 日本製 無香料 シューケアキット 靴 消臭 パウダー (1本)](https://m.media-amazon.com/images/I/41m8Ig2XigL._SL500_.jpg)
![よーく聞いてね!3つのヒントで学ぶ!どうぶつカード ([バラエティ])](https://m.media-amazon.com/images/I/51zT3OcliFL._SL500_.jpg)