合体したブラックホールの表面積はどうなる?
本題といいつつ、ここでもう一度、単純なたとえ話をしましょう。
私たちが部屋選びをするとき、広い部屋を借りようとすると、「いやいや、冬寒いよ」なんて意見を聞くことがあります。
広い部屋を暖房で温めることは、狭い部屋より大変だということは、別に物理学を学んでいなくても、誰でもすぐに理解できる問題です。
しかし、ここでは先程学んだエントロピーを使って、この問題を考えてみましょう。
温度は熱エネルギーであり、寒いということは熱エネルギーが低いということを意味します。
熱エネルギーが低い状態というのは、運動エネルギーが高い分子が散らばってしまい、無秩序な状態になっていることを意味します。
広い部屋と狭い部屋をイメージしたとき、狭い部屋なら熱い分子はあまり散らばらず、秩序をもたせやすいということが想像できます。
逆に広い部屋なら、熱い分子はあちこちに散らばって無秩序になってしまうでしょう。
つまり、広い部屋のほうがエントロピーが高いので、暖まりにくいと考えられるのです。
これはつまり、エントロピーという量は、体積に比例していると考えることができます。
では、ここでもう1つ、イメージを働かせてみましょう。
冬に旅館に泊まったときを想像してみてください。
その旅館の部屋は、食事をする居間と布団を敷いた寝室が襖で分けられています。居間と寝室は同じ広さの部屋です。
居間は暖房を効かせていてとても暖かくなっていますが、寝室は無人なので暖房をかけていませんでした。
このとき、「じゃあそろそろ寝ましょうか」と寝室の襖を開けると、部屋はどうなるでしょう?
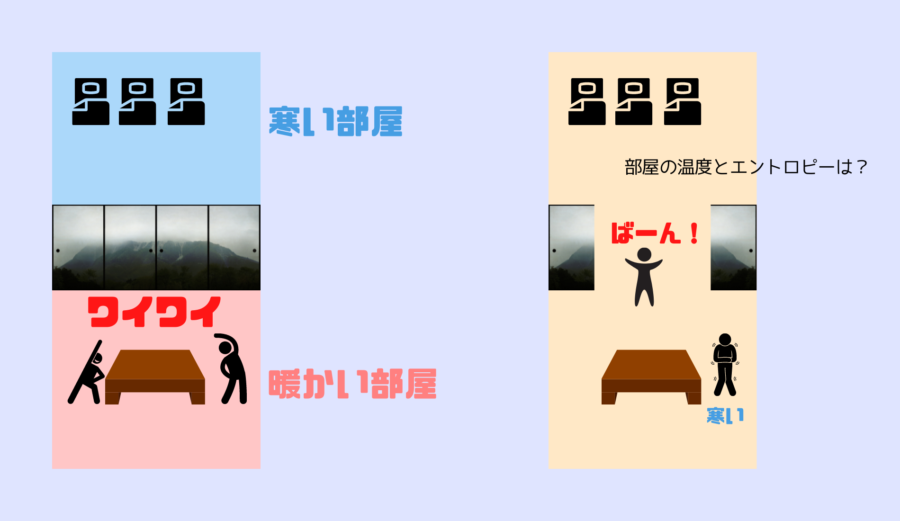
襖を開いたとき、部屋の体積は2倍に広がります。
暖かい空気は、冷たい寝室に流れ込み広がった空間に拡散して非常に混沌とした状態になります。
このとき部屋のエントロピーは、襖で仕切られていた狭い部屋がそれぞれ持っていたエントロピーの和よりも、もっとずっと高い状態になっているはずです。
ここが重要なポイントです。
エントロピーを持った個別の空間が合わさったとき、それは単純に両者の和にはならず、それよりも大きくなってしまうのです。
では今度こそ本題に入りましょう。
エントロピーを表面積として保存する2つのブラックホールが合体したとき、新しく生まれた融合ブラックホールの表面積はどうなると予想できるでしょうか?
そう、合体したブラックホールの表面積は、2つのブラックホールの表面積の和よりも大きくなってしまうと予想されるのです。






























![[W.P.S.] 防水スプレー 除菌 抗菌 防汚 機能付き 大容量420ml 日本製](https://m.media-amazon.com/images/I/41aHfy9uuZL._SL500_.jpg)

![[WILL CLENS] シューズパウダー 日本製 無香料 シューケアキット 靴 消臭 パウダー (1本)](https://m.media-amazon.com/images/I/41m8Ig2XigL._SL500_.jpg)
![よーく聞いてね!3つのヒントで学ぶ!どうぶつカード ([バラエティ])](https://m.media-amazon.com/images/I/51zT3OcliFL._SL500_.jpg)