フィボナッチ数列と黄金比
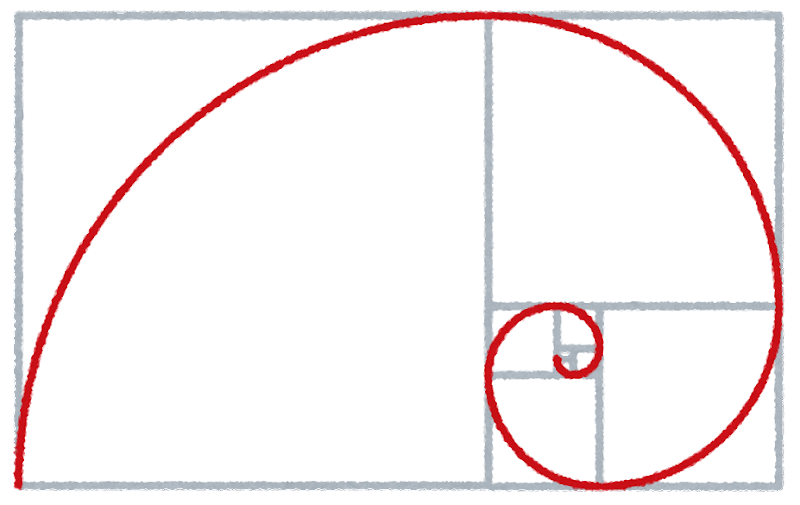
先ほどまで考察していた「各月のウサギのつがいの合計」を並べると
1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,…
という、連続する2つの項を足すことで、次々と数が求まっていく数列が現れます。
これこそが「フィボナッチ数列」です。
とてもシンプルな数列ではありますが、たくさんの面白い性質が隠されています。その一つを見ていきましょう。
フィボナッチ数列の前後の項の比を計算してみます。すると……
$$
\begin{align*}
\frac{1}{1}&=1\\
\frac{2}{1}&=2\\
\frac{3}{2}&=1.5\\
\frac{5}{3}&=1.666666\cdots\\
\frac{8}{5}&=1.6\\
\frac{13}{8}&=1.625\\
\frac{21}{13}&=1.6153846153846\cdots\\
\frac{34}{21}&=1.6190476190476\cdots\\
\frac{55}{34}&=1.6176470588235\cdots\\
\frac{89}{55}&=1.6181818181818\cdots\\
\frac{144}{89}&=1.6179775280898\cdots\\
\frac{233}{144}&=1.6180555555555\cdots\\
\end{align*}
$$
となります。どうやら、1.618くらいの数に近付いているようですね。
実は、フィボナッチ数列の前後の項の比は
$$
\phi = \frac{1+\sqrt{5}}{2}=1.6180339887\cdots
$$
に、限りなく近付いていくことが知られています。
このφ(ファイ)は「黄金比」と呼ばれている値です。黄金比は、古代の芸術品などから見出すことができると言われています。
フィボナッチ数列が黄金比と関係している要因は、その一般項(第n項をnの式で表したもの)を見てみるとわかります。
フィボナッチ数列の一般項は
$$
\frac{1}{\sqrt{5}} \Bigl\{\Bigl(\frac{1+\sqrt{5}}{2}\Bigr)^n-\Bigl(\frac{1-\sqrt{5}}{2}\Bigr)^n\Bigr\}=\frac{\phi^n-(1-\phi)^n}{\sqrt{5}}
$$
で表され、式の中に黄金比が含まれているのです。
この一般項には、二次方程式
$$
x^2-x-1=0
$$
が関わっており、その解が
$$
x=\frac{1\pm\sqrt{5}}{2}
$$
つまり
$$
x=\phi,\ 1-\phi
$$
となっています。
一般項の求め方は、ここでは割愛しますが、興味がある方はぜひ調べてみてくださいね。
今回紹介した黄金比との関連以外にも、フィボナッチ数列には面白い性質がたくさんあります。
たとえば、フィボナッチ数列は、ひまわりの種の螺旋の本数などにも関わっていると言われており、自然界との関連性がよく話題にあがっています。
ほかにも、パスカルの三角形との関係や、類似の数列(トリボナッチ数列やリュカ数列など)も、とても興味深いテーマです。
ぜひ、計算してみたり、調べてみたりしながら、フィボナッチ数列の深みを楽しんでみてくださいね!
<補足>
本記事の一般項では、第1項を1、第2項を1、第3項を2、第4項を3、第5項を5…としているため、うさぎのつがいの問題の「nヶ月後」とはズレが生じています。0ヶ月後が1つがい、1ヶ月後が1つがい、2ヶ月後が2つがい、3ヶ月後が3つがい、4ヶ月後が5つがい…となるので、1つスライドする形になっています。






























![[W.P.S.] 防水スプレー 除菌 抗菌 防汚 機能付き 大容量420ml 日本製](https://m.media-amazon.com/images/I/41aHfy9uuZL._SL500_.jpg)
![よーく聞いてね!3つのヒントで学ぶ!どうぶつカード ([バラエティ])](https://m.media-amazon.com/images/I/51zT3OcliFL._SL500_.jpg)




























