ウサギのつがいの合計を計算してみると……
うさぎのつがいの問題の12ヶ月後までを表にすると、以下のようになります。
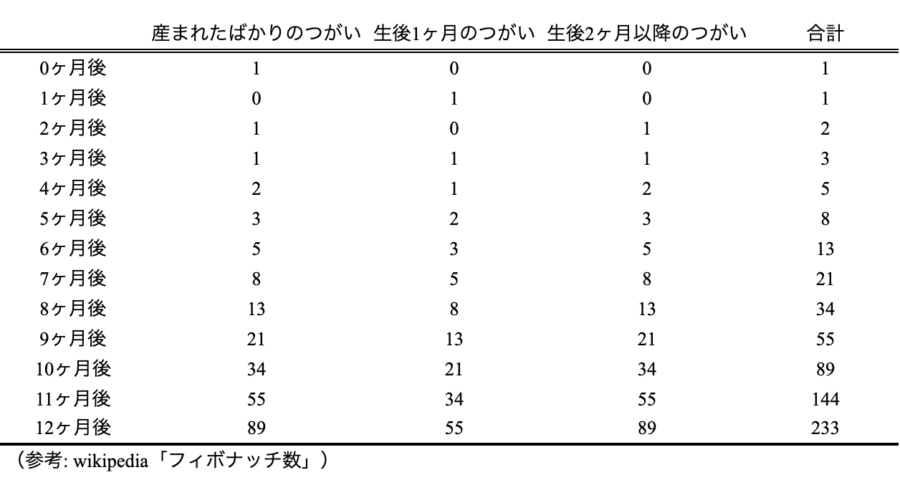
したがって、問題の答えは233つがいとなります。最初は1つがいしかいなかったのに、1年でずいぶん増えましたね！
では次に、合計の部分を抜き出してみましょう。
すると
1,1,2,3,5,8,13,21,34,55,89,144,233
となります。
ある規則性が隠れていることに気づきましたか？
1+1=2、1+2=3、2+3=5、3+5=8、5+8=13、8+13=21、13+21=34…というように、連続する2つの項を足すことで、次々に数が求まっていくのです。
なぜ、このような規則性が現れるのでしょうか？
nヶ月後、(n+1)ヶ月後、(n+2)ヶ月後に注目しながら、調べてみましょう。
まず、(n+2)ヶ月後に産まれるつがいの数を考えてみます。
先ほどの③より
「(n+2)ヶ月後の産まれたばかりのつがいの数」=「(n+2)ヶ月後の生後2ヶ月以降のつがいの数」
となります。
また、nヶ月後に存在するつがいたちは、(n+2)ヶ月後には生後2ヶ月以降となることから
「nヶ月後のつがいの合計」=「(n+2)ヶ月後の生後2ヶ月以降のつがいの数」
となります。
以上より
「(n+2)ヶ月後の産まれたばかりのつがいの数」=「nヶ月後のつがいの合計」 …(a)
であることがわかります。
次に、(n+2)ヶ月後に生後1ヶ月以降となっているつがいの数を考えてみましょう。
(n+1)ヶ月後に存在するつがいたちは、(n+2)ヶ月後には生後1ヶ月以降となることから
「(n+2)ヶ月後の生後1ヶ月以降のつがいの数」=「(n+1)ヶ月後のつがいの合計」 …(b)
であることがわかります。
したがって
「(n+2)ヶ月後のつがいの合計」=「(n+2)ヶ月後の産まれたばかりのつがいの数」+「(n+2)ヶ月後の生後1ヶ月以降のつがいの数」
であることから、(a)(b)より
「(n+2)ヶ月後のつがいの合計」=「nヶ月後のつがいの合計」+「(n+1)ヶ月後のつがいの合計」
となるのです。
