ダ・ヴィンチが仕掛けた「正三角形」の謎
1490年頃、ダ・ヴィンチはある奇妙な人体図を描きました。
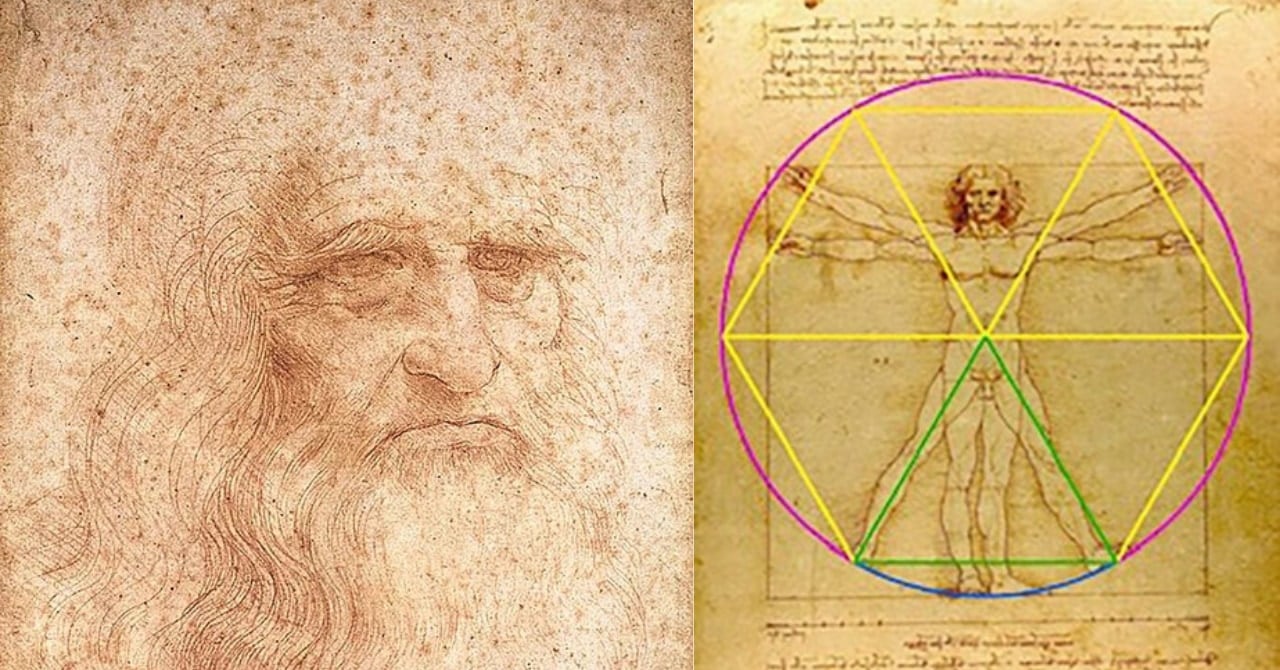
円と正方形の中に、手足を広げた裸の男性がぴたりと収まるあの有名すぎる絵、「ウィトルウィウス的人体図」です。
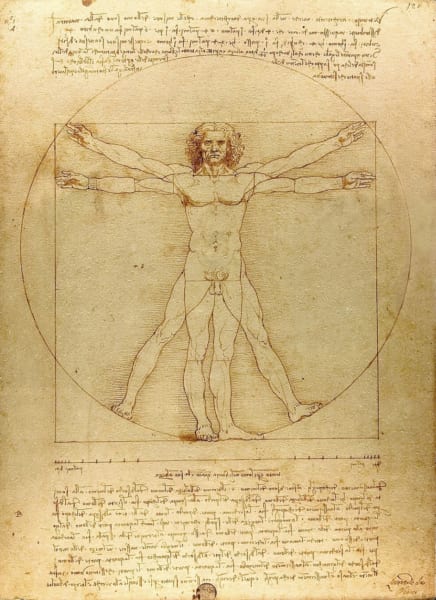
この図は、古代ローマの建築家、マルクス・ウィトルウィウス・ポッリオ（紀元前80年/70年頃 〜紀元前15年以降）が「人間の身体には、よく設計された神殿のように、調和の取れた比率があり、人体は円と正方形の両方に完璧に収まる」と記した考えを参考にして、ダ・ヴィンチが描いたものでした。
しかし、ウィトルウィウス自身はその理論を“どうやって図にするか”についての数学的な方法は残していません。
つまり、ダ・ヴィンチがどうやってこの人体図を完成させたのかは、長年謎だったのです。
この問題に多くの研究者が挑戦し、「黄金比（1.618…）を使ったのではないか（※ 黄金比は約1.618:1の比率で、最も美しいとされる比率の一つ）」とする主張もなされましたが、決定打には至っていません。
そんな中、英国の歯科医、ロリー・マクスウィーニー氏が注目したのは、ダ・ヴィンチが残した手書きのメモでした。
そこにはこう書かれていたのです。
「脚を開いたとき、その空間は正三角形となる」
この「正三角形」こそが、ダ・ヴィンチの幾何学の秘密を解く鍵でした。
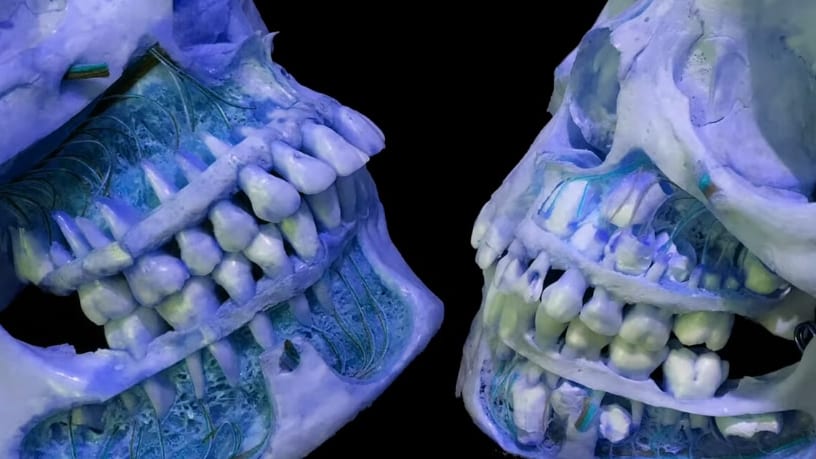
そしてマクスウィーニー氏は、この三角形が1864年に歯科医ボンウィルが提唱した「ボンウィルの三角形」とほぼ一致することを見出します。
ボンウィルの三角形とは、歯科解剖学のなかで知られ、下あごの左右の関節と前歯の中心を結ぶ三角形のことで、理想的な咬み合わせやあごの動きの設計に使われています。
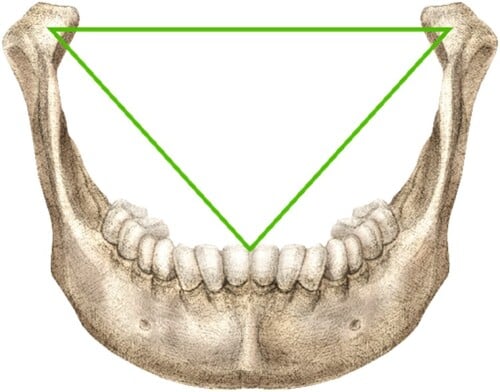
驚くべきことに、この三角形を元に図を構成すると、ウィトルウィウス的人体図に見られる正方形の一辺と円の半径の比率が1.64〜1.65となったのです。
これは自然界で効率的な構造の設計に広く見られる特別な比率「1.633」に非常に近い数値でした。
では「1.633」は自然界においてどれほど重要な数値なのでしょうか？
