黄金比と関係のある数列
黄金比は数学的にも美しいとされています。私たち人間はルールのある数列に心地よさを感じるものです。
例えば
①1,2,3,4,5,6,7,8…
②26,3,408,79,44,2,9…
①と②であれば、どちらの数列を心地よいと感じますか？
多くの方が①と答えるでしょう。なぜなら、数列にルールがあり、それを理解できるからです。
これと同じように、ルールのある数列の中にフィボナッチ数列というものがあります。これには「前の2つの数を加えると次の数になる」というルールがあります。
数学的に美しいフィボナッチ数列は、黄金比と深い関係があります。数列の隣同士の比率を考えると、黄金比である「1：1.6180339887……」に近づいていくのです。
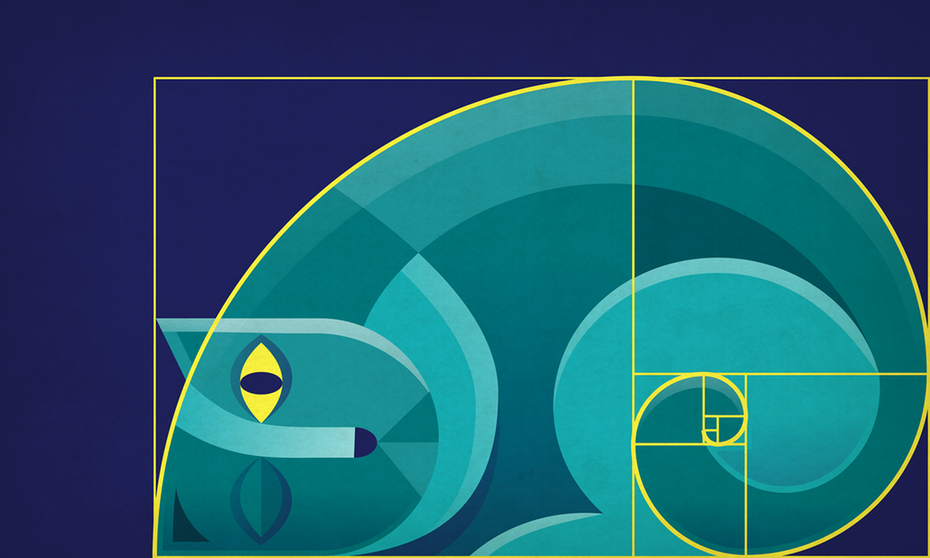
黄金比とフィボナッチ数列の関係性は図形で考えるとより分かりやすくなります。フィボナッチ数列の数字を1辺とする正方形を並べると何になるでしょうか？
図のように、「黄金長方形」になりますね。このことは、黄金比とフィボナッチ数列の深い関係を示しているだけでなく、私たちが黄金比による図形を美しいと感じる理由の証明ともなっています。
人間が黄金比によるデザインを美しいと感じるのは、その中に数列的ルールを見出すことが出来るからでもあるのです。
