「ありえない」粒子の実在性が示される：フェルミオンでもボソンでもない (2/2)

数学の力で「ありえない粒子」をあぶり出す

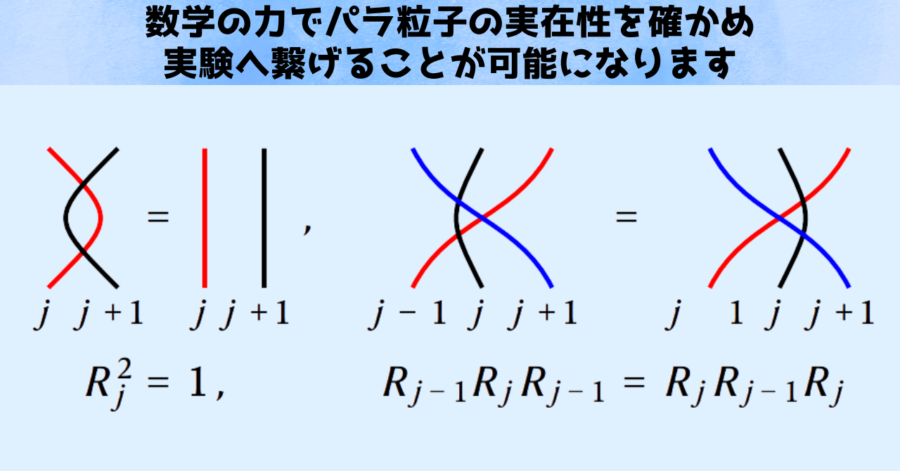
観測が困難だったパラ粒子をどうやってあぶり出すのか？

研究チームはまず理論の組み立てからはじめ、従来の考えにアインシュタインの理論を組み込み、光より速い情報伝達が起きないことや、時間変化が破たんしないこと（ユニタリティー）といった原則を守りながら、パラ粒子を「自由粒子」という扱いやすい形に整理しました。

これまで「どうせ観測できない」と思われていたパラ粒子を、実際に物質の中で“集団の振る舞い（準粒子）”として観測できる場合、どんなものになるかシナリオを描いたのです。

さらに、研究者たちは量子スピンモデルというシンプルな理論空間を用意し、シナリオ通りにパラ粒子が振る舞うかを検証しました。

具体的には1次元や2次元のスピン鎖（たとえば、整然と並んだコマのようなものをイメージしてください）をコンピュータで再現し、その中でパラ粒子らしい交換統計が自発的に生まれる様子を検証しました。

そして大事なのは、これらがただの数式上のお話ではなく、実験によって検証できる形でデザインされていることです。

もし特定の材料や測定技術をそろえれば、スピン系のエネルギーの模様（励起スペクトル）や衝突実験（散乱）を通じてパラ粒子の足跡を追えるかもしれないといいます。

これは「フェルミ粒子でもボース粒子でもないような粒子は、結局同じに見えてしまう」という古い定説をくつがえす挑戦であり、量子の世界に新しいルールがあると証明できるかもしれない、というわけです。

さらに論文著者であるワン氏とハザード氏は、パラ粒子が準粒子ではなく基本粒子として存在する可能性についても述べています。

もしパラ粒子が基本粒子として存在するならば、標準理論が唱える2元論に挑むものになるでしょう。

英国リーズ大学のジャンニス・パチョス氏は、「彼らが示した準統計の存在可能性は、科学の歴史に残る画期的な成果だ」と述べ、研究の重要性を強調しました。

さらに、この研究は哲学的な問いを呼び起こします。

私たちが物理学で観測する現象は、本当に宇宙の全貌を反映しているのでしょうか。

それとも、観測可能な現象は、より広大な真実の一部に過ぎないのでしょうか。

この問いは、科学がどのようにして未知を追求し続けるかという根本的な問題にも関連しています。

この議論はまた、一般の人々にとっても重要な意味を持ちます。

私たちが理解している宇宙の仕組みが、これまで考えられていた以上に複雑であることを示唆しているからです。

研究者たちは、今後さらに多くの実験を通じて理論を検証し、この未知の領域を探求する予定です。

技術的な側面では、パラ粒子は量子コンピュータのエラー耐性を強化する可能性があります。

従来のフェルミ粒子やボース粒子とは異なる統計特性を持つこれらの粒子は、新しい物質の設計やトポロジカル相転移の研究にも役立つでしょう。

研究者たちは「パラ粒子が実際に現れて、かつ観測される可能性を示すのは非常に興味深い。量子コンピューティングへの応用を視野に入れるなら、こうした新しい粒子統計はエラー訂正や情報符号化の仕組みを根本から変えるポテンシャルがあるでしょう」と述べています。

しかし、この分野にはまだ多くの未解決の課題があります。

特に、3次元でのパラ粒子の実現可能性や、それが自然界に存在する証拠を見つけることは、次の大きな挑戦となるでしょう。

ワン氏自身も「実験で証明するにはより現実的な理論的提案が必要になるだろう」と述べています。