数学的難問「ABC予想」がついに解明！ABC予想の基本と成果をやさしく解説してみた

カンタン？なABC予想解説！

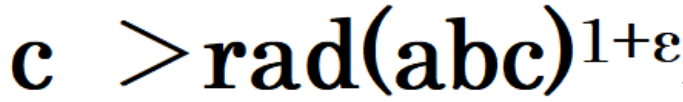
ABC予想とは、3つの自然数の特別な関係を証明したものになります。

予想がどのようなものであるかを理解するには「rad」という、簡単な概念を理解するだけで十分です。「rad（●）」とは、「●の部分にある数字の中にある素数だけを掛け合わせて下さい」という記号で、「根基 (radical) 」の略です。

大丈夫です。すごーく簡単で、簡単すぎることをなんでこんなに難しく書くんだ？　と問いたくなるレベルですから。

ではまずは、「rad(8)」を例にとります。

8は2の3乗なのでrad(8)はrad(2³)と書き直すことができます。

ここまでは、大丈夫ですよね？

流石に8=2³がわからない人は…いません、よね？

このときrad(2³)の答えは、乗数を無視して「2」になるんです。

rad(2³)=「2」

え、それだけ？

と思うかもしれませんが、「rad」はそれだけの簡単な概念なのです。

同じように、

rad(25)はrad(5²)となり、答えは乗数を無視した「5」になります。

またrad(50)など乗数だけでは表せないものについては、掛け算の組み合わせに分解します。

つまり…

rad(50)=rad(25×2)=rad(5²×2)となり、あとは乗数を無視して掛け算（5×2）を行い、rad(5²×2)=5×2=10となります

またrad(45)のときは…

rad(45)=rad(9×5)=rad(3²×5)=3×5=15

になります。

さて、radがわかったところで、いよいよABC予想の根幹を示します。ABC予想とは、3つのa,b,cという数が、任意（適当）の数「ε」のもとに、

という数を満たす「a,b,cの組み合わせが、ほんの数個しかないことを証明する問題」だったのです。

radの次のカッコの中に「abc」と固まっている部分は「a×b×c」という意味です。

一見すると、簡単に証明できそうですね。

でも、誰も証明できなかったんです。そう、望月教授を除いては。