時空はより高度な概念の投影に過ぎない：コスモヘドラで時空は消える

“宝石のような図形”で物理法則を語ることができる

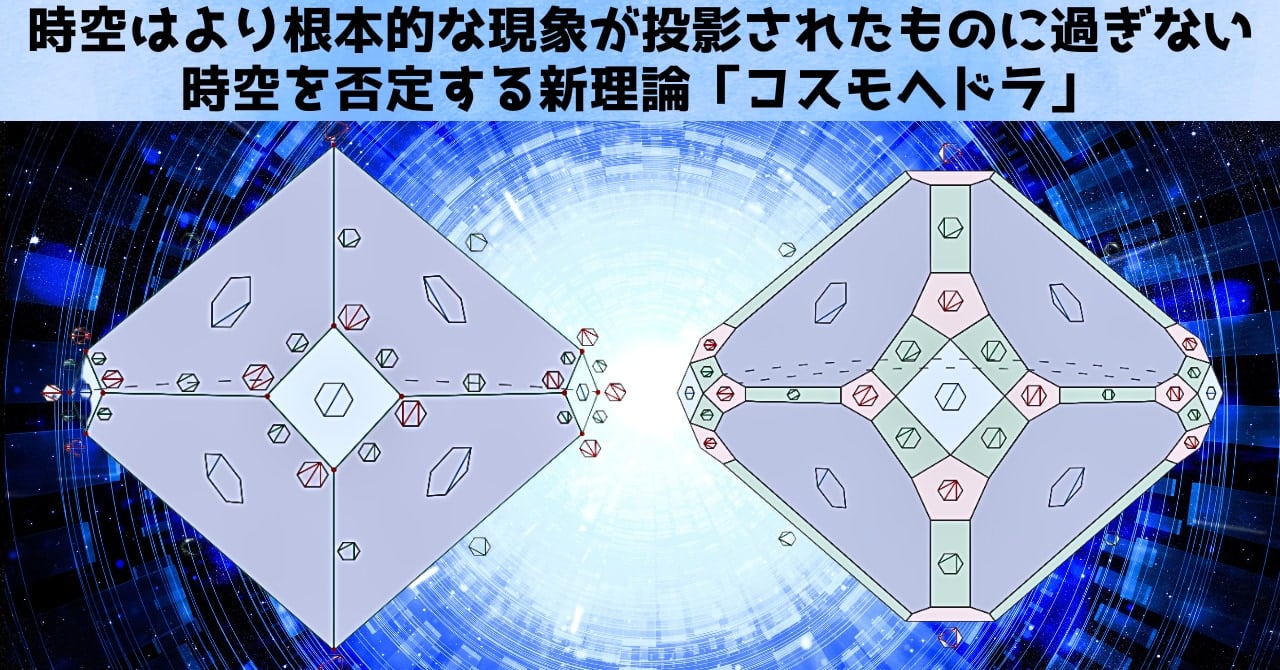
「コスモヘドラ（Cosmohedra）」については、まずはまるで“宝石”のような多面体──角ばった結晶のイメージを思い浮かべると分かりやすいでしょう。

このコスモヘドラは現在、宇宙全体の量子波動関数を一挙に再現できるかもしれないという、ちょっと信じがたいほど壮大な狙いをもって研究されています。

といって、いきなり「宇宙の波動関数を宝石の形で表す」と言われても、イメージが湧きにくいかもしれません。

そこでまずは、このコスモヘドラの“前身”ともいえるアッソシアヘドロン (Associahedron)を例に、考え方の大枠を見ていきましょう。

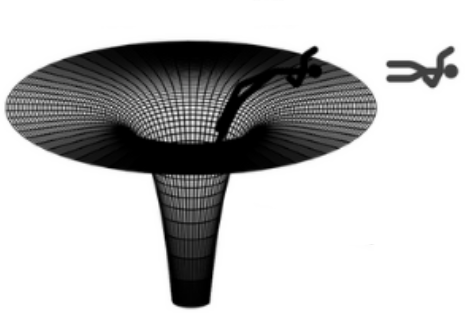
ここではまず空間を飛び回る粒子を、時空を前提とした計算式で表すことからはじまります。

たとえば、私たちが日常で想定している「時空」という座標系を使って粒子の衝突（散乱）を厳密に計算すると、時間と空間の情報を余すところなく書き下さなければならず、その手順は膨大になりがちです。

「いつ」「どこで」「どのように」衝突が起こり、衝突後は「どの向き」に粒子が飛ぶのか……そうした要素をすべて数式で扱うには、莫大な計算が避けられません。

ところが、近年登場した「陽的幾何（positive geometry）」という発想や、高度化したシミュレーション技術の応用によって、最終的な運動量分布を「多面体の形状」として一括管理できることが分かってきたのです。

（※陽的幾何は、数々の物理条件をまとめてう形で表し、その図形的性質を読むだけで重要な物理量が分かる、という優れた手法です。煩雑だった方程式が一つの美しい形に凝縮されるという、エレガントな魅力があります。）

例えるならば、「巨大なデータファイル（粒子の衝突情報）を、きれいに圧縮した多面体のファイルに変換しておき、そこから必要な情報を読み出すだけで元のデータを再現できる」というイメージに近いでしょう。

実際、アッソシアヘドロンを使うと数千行にもおよぶ膨大な方程式がぐっと短縮され、しかも結果が変わらないことが分かっています。

いわば、「複雑な数式を根気よく解くかわりに、決められたルールで作ったポリゴンや多面体の“辺”や“面”、“体積”を読み取れば事足りる」というわけです。

簡単に言えば「全体を覆う多面体の情報に内部の粒子の情報を全てコンバートでき、多面体の測定により内部粒子の状態をも知ることができる」ということがわかったのです。

その多面体の“辺や面、体積”といった幾何学的な性質が、実は膨大な方程式の答えと一対一に対応しているからです。

たとえば「この面に相当するのは〇〇という衝突パターン」「この体積を求めると、衝突全体の寄与が一気にわかる」といった具合です。

（※「もともと広がった空間・データを、よりコンパクトな境界・図形構造に落とし込み、それを読むだけで元の情報が再現できる」という点においてはホログラフィック原理を連想させる仕組みでもあります。）

ここで面白いのは、こうした計算過程でいったん「時空」（座標や時間の情報）を明示的に使わないことです。

“多面体がもつ純粋な幾何学的性質”を頼りにして、「結果的に従来の方程式と同じ答えを導き出す」仕組みを利用しているのです。
実際にやってみると、時空の座標を延々と追っていたよりも遥かにスマートに問題が解ける場合がある。

まさに、宝石のような図形ひとつで、物理学の煩雑な方程式を“置き換えてしまう”かのような感覚です。

便利と言えば、間違いなく便利でしょう。

しかしこの成果は、単に便利な計算テクニックをみつけたという話ではありません。

時空の存在をベースにした従来の大量の方程式を、時空の存在を考えず設定された多面体の測定だけで解けるという事実は、時空がなくても物理学は何とかなる……つまり時空はより根本的な何かの投影に過ぎない可能性を示しています。

この流れで登場する最新の形が「コスモヘドラ」。

アッソシアヘドロンは“粒子の衝突”に焦点を当てたものでしたが、コスモヘドラはもっとスケールが大きい──宇宙全体（“宇宙の波動関数”）を記述できるようにデザインされています。