バタフライ効果と天気予報
カオス現象の持つ「ある物理的な対象にわずかな変化を与えると、その後の状態が大きく異なり予測できない現象を見せる」という特性はバタフライ効果という名前で呼ばれることもあります。
この単語は様々な漫画やアニメ、映画などで使われているため聞いたことがある方もいらっしゃるかもしれません。
このバタフライ効果という表現は、気象学者のエドワード・ローレンツが1972年にアメリカ科学振興協会で行った講演のタイトルに用いられた「ブラジルの1匹の蝶の羽ばたきはテキサスで竜巻を引き起こすか？」という表現に由来すると考えられています。
ここでいう蝶の羽ばたきは小さな変化、すなわち初期値のわずかな差を意味しています。
そんな僅かな初期値の差が、ブラジルから遠く離れたテキサスで竜巻を起こしてしまうかもしれない。
これはあくまで極端な例題ですが、蝶の羽ばたきからは想像できないような大きな影響が生じるかもしれない、というカオス現象を考えることの難しさを「バタフライ効果」は簡潔に表現していたため、世界的に有名な用語になりました。
バタフライ効果はローレンツが気象学者であったことからも分かるように、元々は天気予報という日常生活に馴染みのある分野の予測不可能性を説明するために生まれた言葉です。
天気予報では流体力学の運動方程式をモデル化することで予測を行っています。
ところがこの運動方程式の解はカオスの性質を持っており、ローレンツが主張した通り決定論的に未来を見通すことは不可能でした。
運動方程式の厳密な解を求めるための初期値やモデルが分からないだけでなく、誤差がどれほど大きくなるかも予測が難しく、事前に知ることはできません。
しかしそうはいっても、現在の天気予報は数日程度であればかなり正確に行うことができます。
いかにして人類はこれを実現させたのでしょうか？
現在の天気予報では「アンサンブル（集団）予報」という手法を利用しています。
この手法では、まずある時刻に少しずつ異なる初期値を多数用意するなどして多数の予報を行います。
それらを用いて、平均やばらつきの程度といった統計的に情報を得ることにより気象現象の発生を確率的に捉えることが可能となります。
こうすることにより予測の信頼性を事前に推定できるようになりますし、複数のデータを用いることにより可能性のあるシナリオを複数予測することも可能になります。
現在は予報する期間や用途によって様々な予報システムを使い分けています。
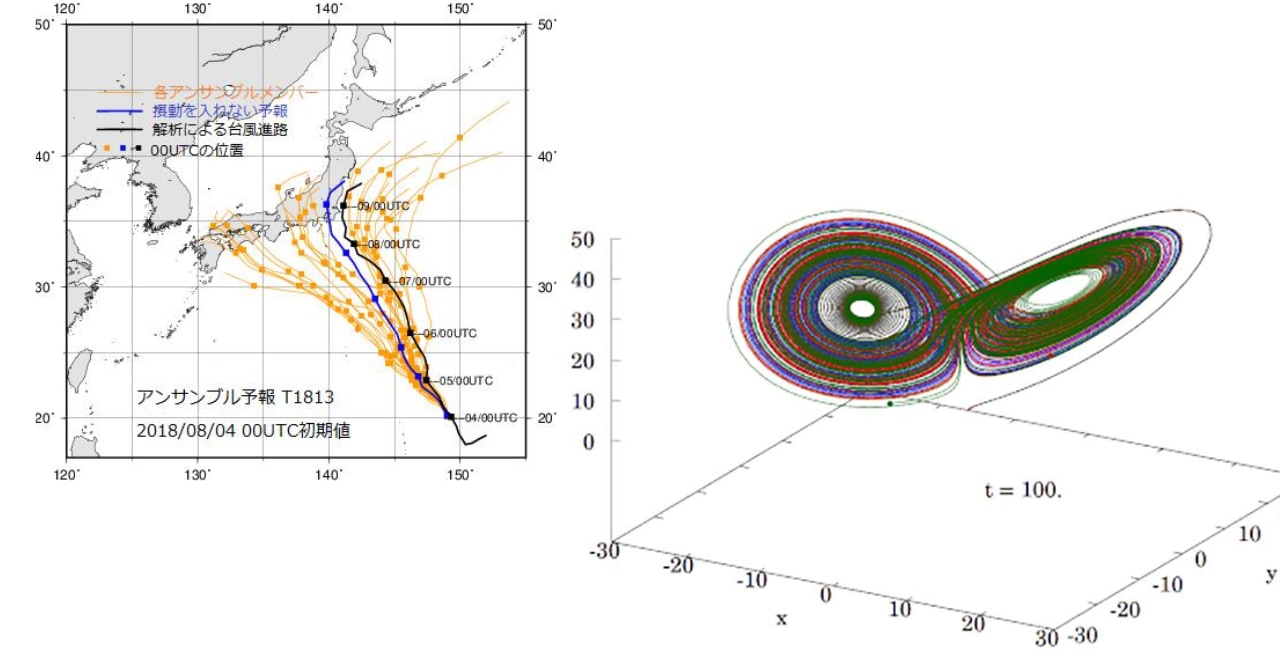
下図は、2018年8月4日9時を初期値とした台風第13号の進路の5日予報です。
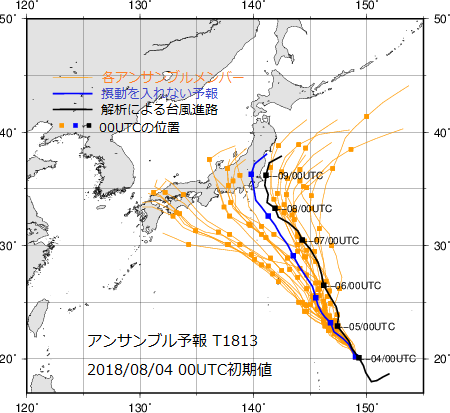
黒色の線が実際に台風が通った進路で、橙色の線は初期値を様々に変えて誤差を考慮した予測です。
また青色の線は初期値に含まれる誤差を考慮しなかった場合の予測となっています。
橙色の線と黒色の線を見比べると、実際の進路が予測のばらつきの範囲内に含まれていることがわかります。
初期状態のわずかな違いで時間とともに台風の取る可能性のある進路が広がっていきます。
しかし、これらのデータを複数集めて統計的に扱うことで、予測が当たる可能性を上げているのです。
