時間が遅くなる仕組みとは?
まずは、昔は時間が変化しないと思われていたことから説明する必要がある。
いまでこそ時間は相対的なもので、あなたにとっての「今」と私にとっての「今」は違うことがわかっているが、100年ちょっと前までは「時間は絶対的なもの」だと信じられていた。
世間の認識がひっくりかえったのは、1905年にアインシュタインが特殊相対性理論を発表してからだ。
アインシュタインによれば、「時間(や空間)は相対的で変化するもの」なのだ。
でもアインシュタインが突然「時間が相対的なもの」というアイデアを思いついたわけではない。
アインシュタインがすごいのは、いままで変化すると思われていた光の速度を「変わらない唯一の速度」と定義したことだ。
そして光の速度に近づくほど、時間の進み方が遅くなるとした。
このあたりを説明するために、普通は光を媒介すると考えられていたエーテルやマイケルソン・モーリーの実験を紹介していくのだが、私はシンプルにいきたいのでバッサリ省略する。気になる方は検索してください。
さっそく「時間の遅れ」を計算する数式を紹介しよう。
まず読み方を左から説明すると、⊿(デルタ)は「ごくわずか」、tは「時間」、vは「速度」、cは「光の速度」を意味する。
右のごくわずかな時間tに√の中をかけると、左のごくわずかな時間Tに変換されるという式だ。
※なぜわざわざごくわずかな時間にしているかと言うと、瞬間的な時間であればその間の速度変化を考えなくてよいので、お手軽な慣性系で計算できるからだ。
(1)の式を日本語で解説すると、
どうだろう? 少しはわかりやすくなっただろうか?
なかなかイメージできない? それではこの式がどうやってできたのかを説明しよう。
難しい式を使うのかと思いきや、なんと中学校で習うピタゴラスの定理(三平方の定理)から説明できるのだ。
次の図を見て欲しい。
地球にいるAさん(止まっている人)から、ロケットに乗って光の速度(30万km/秒)に近いスピードで飛んでるBさん(動いている人)を見たとしよう。
Bさんのロケットがvの速度で飛んでいて、BからB’の位置までくるのにt時間かかったとするとB-B’間の距離は「道のり=速さ×時間」だから「vt」と表わすことができる。
ちなみにA-B’間の距離は、Aさんが観測する光の速さcとBからB’までの時間tをかけたものだから「ct」。
残ったA-B間の距離は、止まっているAさんから動く前のBの位置にいたロケットまでの時間をTとすると、光の速さは不変なのでさっきのcを使って「cT」となる。
さっきの図に書き込むと、

注目したいのはcT間の距離にくらべ、ct間の距離が斜めに延びていることだ。
光速度不変の原理より、c(光)の速度は変わらないので、延びた分だけ時間が遅くなってしまうのだ。
さてこの理屈がわかったら、次はピタゴラスの定理を思い出そう!
上の三角形ABB’はBの直角が辺ABと辺BB’にはさまれた直角三角形なので斜辺AB’はピタゴラスの定理から次のように計算できる。
辺ABを「cT」、辺BB’を「vt」、辺AB’を「ct」に置き換えて計算すると、
両辺からv2t2を引くと、
両辺をc2で割ると、
右辺のt2を( )でまとめて、両辺に正の平方根をとると
ほら(1)の式になった!
それではいよいよ時間の遅れを計算してみよう。
日本語にした(2)の式に具体的な数値を入れてみる。
光の速度は約30万km/秒、Bさん(動いている人)のロケットはその2/3の速さ20万km/秒で飛んでいるとする。地球にいるAさん(止まっている人)からすると、
つまりAさんの時間の進み具合はBさんに比べて75%になる。言い換えるとAさんはBさんより1.3倍時間が遅れる。
(2)の式の「動いている人の速度」を変えていろいろ入力すれば、どのくらい時間を遅くできるのかがわかる。
つまり光速度の10%(3万km/秒)ぐらいでは時間はほとんど遅れず、10倍の遅れを体感するには光速度の99.5%(29.85万km/秒)というとんでもないスピードが必要とされる。
実感するだけの時間の遅れを実現するのは、なかなか難しい。










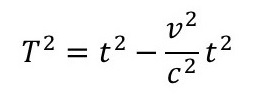
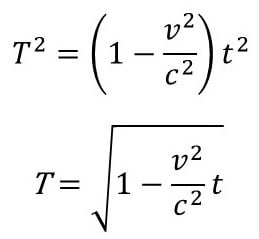


























![[WILL CLENS] シューズパウダー 日本製 無香料 シューケアキット 靴 消臭 パウダー (1本)](https://m.media-amazon.com/images/I/41m8Ig2XigL._SL500_.jpg)

![[W.P.S.] 防水スプレー 除菌 抗菌 防汚 機能付き 大容量420ml 日本製](https://m.media-amazon.com/images/I/41aHfy9uuZL._SL500_.jpg)
![シルバーバック かわいい海の生きもの CUBE 2X2 キューブ ツーバイツー|海の生き物デザイン 立体パズル スピードキューブ 5cm 子ども〜大人向け 知育 ギフトに最適 ([バラエティ])](https://m.media-amazon.com/images/I/41EJOOLgGXL._SL500_.jpg)