観測不能と言われた弦理論を宇宙実験場へ

今回の研究は非常に専門性が高いために、まず最初にざっと解説したバージョンを示します。
弦理論はこれまで数学的なアプローチが主であり、実験によって検証することが極めて困難とされていました。
しかし新たな研究は、ブラックホールのすれ違いの瞬間を観測できれば、弦理論が実際に宇宙に息づいていることを確認できる可能性を示しています。
ざっくり解説
ブラックホールが衝突するときの重力波は大きくて観測しやすいのですが、今回注目されたのは「合体しない」すれ違い(散乱)の瞬間です。
まるで二つの巨大な星が、宇宙の大舞台で軽やかに“かすめ合う”ようにすれ違い、そのわずかな時間に重力波の短いバーストが放出されます。
実はこの“かすめ合い”を正確に計算するのはとても難しく、従来の手法では大ざっぱな見積もりしかできませんでした。
そこで研究チームは、粒子加速器で荷電粒子が散乱するときの計算技術を大胆に応用し、「ブラックホールを一点の粒子とみなす」視点で超精密に解きました。
すると、弦理論で登場する「カラビ・ヤウ多様体」という高度な幾何学構造が、散乱によって出る重力波のエネルギーや軌道の変化を正しく記述するのに不可欠とわかったのです。
これは「難解で観測不可能」と思われていた弦理論の数学が、実在の天体現象を予測する際に必須だったという大きなサプライズです。
この結果は「弦理論は検証が難しい」という一般的なイメージを覆す可能性があり、ブラックホールという超巨大質量天体が生み出す重力波こそが、新たな“実験場”になることを示唆しています。
2030年代に稼働する次世代重力波望遠鏡(アインシュタイン望遠鏡、Cosmic Explorer、宇宙機 LISA)がこの波形を捕え、理論値と合致することを確かめられれば、それは弦理論の中核となる「紙上の六次元ドーナツ」が宇宙で本当に呼吸しているかを決定づけることになります。
(※より厳密には“ブラックホール散乱の 5PM 係数にカラビ-ヤウ多様体の周期が現れる” ことを示しています。著者も「同じ構造は弦理論以外の量子場理論アプローチでも現れる可能性がある」と注意書きを入れており、検証には追加の理論分離と高 S/N 観測が必要と強調しています。)
一般相対性理論によれば、ブラックホールや中性子星など大質量天体が互いにすれ違う際、重力相互作用によって軌道が変化し、重力波が放出されます。
私たちはすでにブラックホール同士の衝突(連星合体)に伴う重力波を数多く観測してきましたが、一方でこうしたすれ違いざまの散乱による重力波の詳細な予測は依然として難しいままです。
ブラックホール同士が衝突せず近距離ですれ違う場合は「散乱」と呼ばれ、重力によるスリングショットのようにお互いを弾き飛ばす現象です。
散乱では合体が起きないため、放出される重力波は短いバースト状になり、ブラックホール同士は再び遠ざかっていきます。
こうした一瞬の重力波信号は連星合体のような長いチャープ信号に比べて捉えづらく、まだ未検出ですが、存在しないと断定はできません。
実際、LIGOやKAGRAなどの現行重力波望遠鏡は今後さらなる高感度化が予定されており、2030年代には欧州の地下観測所アインシュタイン望遠鏡や米国のCosmic Explorer、さらに宇宙重力波アンテナLISAといった次世代計画もスタートする見込みです。
これらの施設が稼働すれば、ブラックホールが合体せず高速ですれ違う散乱イベントによる重力波を初めて検出できる可能性が高いです。
このときに備え、理論面でも散乱イベントの波形を高精度に予測し、「どんな信号を探せばよいか」のテンプレートを準備することが求められています。
今回の研究はまさにこの課題に取り組んだものです。
弦理論は宇宙のあらゆる素粒子や力を一次元の「ひも」の振動モードで説明しようとする仮説であり、典型的には(時間1+空間9)=10次元を想定します。
目に見えない余剰の空間次元は極めて微小に折り畳まれて存在すると考えられ、その有力な折り畳み方がカラビ・ヤウ多様体です。
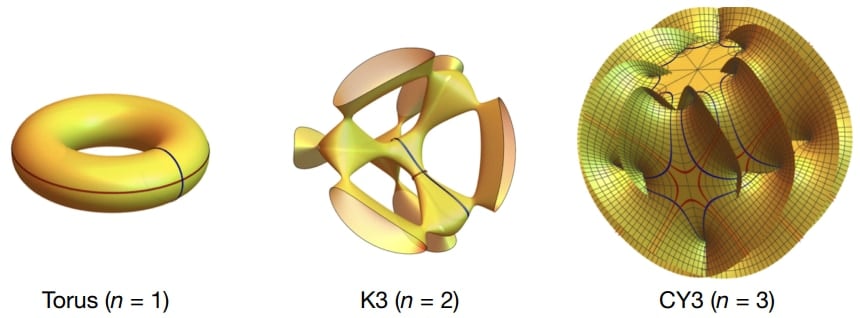
カラビ・ヤウ多様体は特殊な幾何学的性質を備えた空間構造で、複素3次元(実6次元)の“ドーナツ”をさらに複雑にしたようなイメージがしばしば用いられます。
弦理論はこうした追加次元や超対称性などを仮定する一方、直接的な実験証拠に乏しいため、「検証が難しい理論」として批判も受けてきました。
しかし今回のブラックホール散乱研究において、弦理論の核心部分と考えられる数学的エッセンスが重力波現象と直接結びついた可能性が示唆されたのです。
ある意味では、観測が難しいといわれてきた弦理論の要素を、ブラックホールという宇宙最大級の“実験場”で垣間見ることに成功した格好です。