クモの「バルーン化」をシミュレーション
クモがバルーンのように浮遊する仕組みは、おもに2つに分類されます。
1つは、太陽の光に暖められた空気が上昇するとき、クモ糸がその気流を受け止めて揚力を得るというもの。
もう1つは、弱いながらも大気中に常に存在する垂直電場が、糸の静電荷に作用して揚力を得るというものです。
これらはいずれも、糸に作用する力を仮定しています。
専門家はこれまで、この2つの仮説を実験によって検証してきましたが、気流や電場が細く小さなクモ糸におよぼす影響を観察することは困難でした。
UCLAのカリード・ジョード(M. Khalid Jawed)氏は「(過去の研究の)シミュレーションは、糸が複数あれば大きな効果が得られるにもかかわらず、1本の糸のみを想定していた」という。
たとえば、静電メカニズムの場合、揚力は電荷の空間分布に強く影響されるはずで、それは空間における複数の糸の配置によって決定されます。
そこでジョード氏とNDUのシャーベル・ハブチ(Charbel Habchi)氏は、コンピューターグラフィックス業界で開発されたアルゴリズムを使うことにしました。
このアルゴリズムは、『ホビット』や『猿の惑星』シリーズといったハリウッド映画で、毛皮や髪の毛をリアルに再現するために応用されています。
これを使えば、クモの各糸を曲げたり、伸ばしたり、ねじったり、自由に動かすことが可能です。
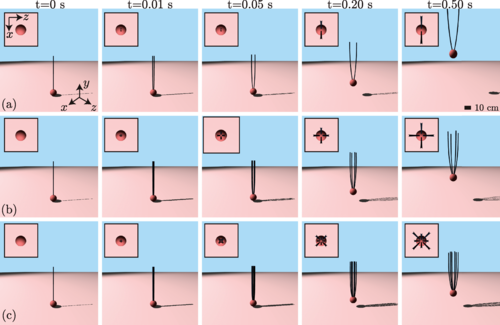
今回のシミュレーションでは、クモの体を幅2mmの球体として仮定し、その上部に糸を取り付け、最初は垂直の状態に置きました。
クモ糸の条件は、2本、4本、8本の3パターンで行っています。(下のシミュレーション動画は、4本の場合)
それぞれの糸は電荷で覆われており、重力や 大気の電場(高さに応じて減少)、糸にかかる空気抵抗なども考慮しました。
シミュレーションではまず、地面に静止しているクモが電場によって上昇します。
すると帯電した糸は、最初はまっすぐな状態でしたが、相互反発によって、時間とともに互いに(膨らむように)離れていきました。
しかし、クモが上方に加速すると、下向きの抵抗が大きくなり、またクモ自体の重さも加わって、最終的に揚力は打ち消されています。
この上昇力と下降力のせめぎ合いが、クモの最終的な上昇速度を決定していたのです。
研究チームは、複数の糸が帯電していれば、電荷や電場がないときのように糸が互いに絡まることはなく、秩序ある配置を保つと結論付けています。
Habchi氏は、次のように説明します。
「少なくとも小型のクモの場合は、上昇気流の助けを借りずに電場によってバルーン化できると考えられます。
しかし、より大きなクモの場合は、電場に加えて、上向きの気流による後押しが必要です」
チームはまた、電荷が糸全体にまんべんなく分布する場合と、糸の先端に局所的に分布する場合でもシミュレーションしました。
その結果、どちらの条件でもクモの持ち上げに必要な力を発生できることが示されています。
本研究の成果について、ハブチ氏は「生物学にとどまらず、環境科学の分野でも新しいデバイスの開発に応用できる」と話しました。
チームは今後、シミュレーションではなく、実際の自然環境におけるクモの飛翔について研究したいと述べています。




























![[W.P.S.] 防水スプレー 除菌 抗菌 防汚 機能付き 大容量420ml 日本製](https://m.media-amazon.com/images/I/41aHfy9uuZL._SL500_.jpg)
![[WILL CLENS] シューズパウダー 日本製 無香料 シューケアキット 靴 消臭 パウダー (1本)](https://m.media-amazon.com/images/I/41m8Ig2XigL._SL500_.jpg)
![よーく聞いてね!3つのヒントで学ぶ!どうぶつカード ([バラエティ])](https://m.media-amazon.com/images/I/51zT3OcliFL._SL500_.jpg)