アリの戦争も「質で数に勝つための条件」が人間と同じと判明！

戦力における「数と質」の問題は種を超えて存在する

古来から戦争の指導者たちは同じ悩みを抱えていました。

「多数の弱い徴兵を送り込むべきか、それとも少数の精鋭戦士を配備すべきか」

前者の場合、農民を徴兵して間に合わせの武器で戦わせる方法と言えるでしょう。

数は容易に揃いますが、農民たちの多くは武器を持ったこともない素人ばかりです。

一方後者の場合、古代ギリシャのスパルタ兵が相当するでしょう。

幼い頃からの厳しい訓練はスパルタ兵を最強の兵士にしました。

しかし裏を返せば1人の兵士を育てるために膨大な時間と労力の投資が求められ、量的な拡大は不可能でした。

人間を使って「戦力」を作る限り、数と質の問題は常に付きまといます。

では、人間ではない場合はどうなのでしょうか？

自然界には人間以外にも、アリやハチなど集団戦を行う種が多数存在します。

その良い例として、オーストラリアのアリ同士の戦争が挙げられます。

在来種である大きな体格を持つオーストラリアアリ（I. purpureus）は現在、小型のアルゼンチンアリ（L. humile）による侵略を受けています。

大柄なオーストラリアアリ（8㎜）は小柄なアルゼンチンアリ（2㎜）よりも体長が4倍、質量に至っては40倍にもなり、高い戦闘力を持ちます。

しかし大きな体を作るにはそのぶん多くのエサが必要（高コスト）となり、コロニーが揃えられる数は限られています。

一方、小柄なアルゼンチンアリは爆発的な繁殖力を備えており、一定段階まで育ったコロニーでは在来種では考えられないような異常な個体数が確認されています。

彼らの場合も、人間と同じように戦力における数と質は作用するのでしょうか？

そこで今回、西オーストラリア大学の研究者たちは、動物の社会で行われる戦争において、数と質がどのように影響するかを、極めてユニークな方法で調べることにしました。

その方法とは、古くから親しまれている戦略ゲーム「Age of Empires2」をベースにしたものでした。

この戦略ゲームではまず、各プレーヤーは自らが属する文明を選択します。

そしてゲームが始まると、周囲の資源を集めながら戦闘ユニットを製造し、ライバルを打ち倒すことを目指します。

また生産にはコストの概念が存在しており、高性能なユニットは高コスト、低性能なユニットは低コストで作成されます。

たとえばドイツ文明が生産する騎士はゲーム中でも最強の戦闘力を持ちますが、作成するのにも大きなコストがかかります。

そのため最強の騎士軍団を作ろうとしても、十分な数が揃う前に、平凡な戦闘力しかない剣士の群れに襲われて負けてしまうことがあります。

戦略ゲームでは素早く低コストのユニットを生産して相手の準備が整う前に攻撃する方法が有効であることが知られており、プロゲーマー同士の戦いではしばしば「最強の騎士軍団」が登場する前に勝負がついてしまうことさえあります。

研究ではまず、この騎士（高コスト）と剣士（低コスト）にさまざまな条件で戦闘を行わせ、データを集計することからはじめられました。

すると騎士1体に対して剣士１～４体を戦わせた場合には常に騎士が勝利し、逆に騎士1体に対して剣士5～10体を戦わせた場合には常に剣士側が勝利しました。

次に研究者たちは得られたデータを、ランチェスターの法則に当てはめ、騎士と剣士の戦闘力比を算出しました。

ランチェスターの法則は戦力を元に、集団戦闘を行った場合の生存数を予測する法則であり、剣や弓の使用を想定した一次法則と、銃火器の使用を想定した二次法則が知られています。

（※特に二次法則はビジネス書などでも紹介されている有名な法則として知られています）

結果、騎士と剣士の戦闘力比は「0.22」すなわち騎士は剣士の約5倍の戦闘力を持つことが示されました。

次に騎士9体を剣士20～90体と戦わせる、より大規模な戦闘を行いました。

またこの大規模戦闘では「地形の複雑さ」の概念も取り入れられました。

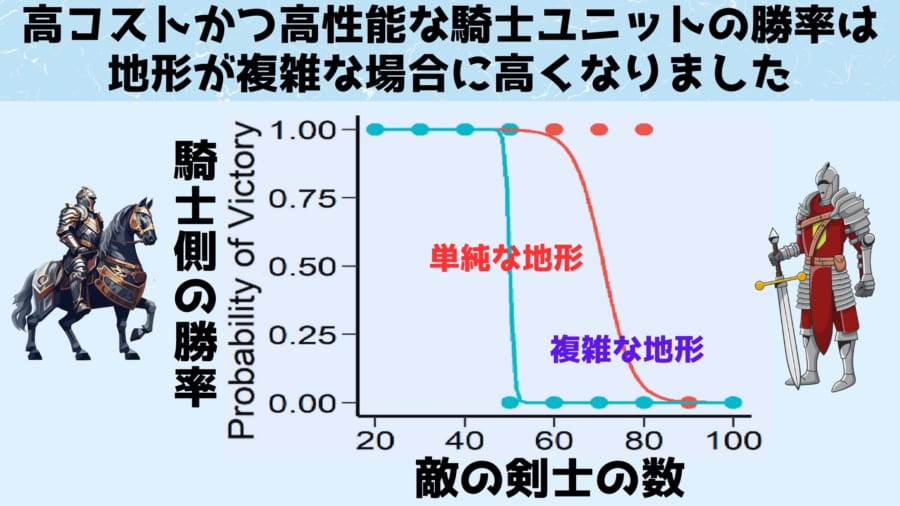
結果、単純な地形の場合、剣士の数が50人を超え始めると騎士の勝率はほぼ0となりましたが、複雑な地形では剣士の数が80人を超えても、騎士側が勝つケースがみられました。

この結果は、複雑な地形には少数精鋭の軍の勝率を上げる効果があることを示しています。

興味深いことに、同じ結果は実際の人間の戦争でも起こり得ます。

戦史を調べてみても、地形が複雑な山間部や谷間、密林のような地形では「大軍が利点を生かせず小規模の軍隊に敗北した」という事例が多数知られています。

ゲームでの分析が終わると、いよいよ本物のアリを使った戦争が開始されました。