この世界に姿がない数字たち
数式は出さないと言っても、話の主役となる数式を見ないわけにはいかないので、まずはその数式を見てみましょう。
$$
e^{i\pi} =-1
$$
これがよく世界で最も美しい数式と言われるオイラーの式です。
この式では右辺の\({-1}\)を左辺に移動させて、\( e^{i\pi}+1=0 \)と答えを\({0}\)にしたバージョンもよく紹介されます。
この場合、答えが\({0}\)に収まるのが美しいと言われたりしますが、この式の本質とはあまり関係がないので、この記事では上の\({-1}\)になる形を基本として話していきます。
おそらくほとんどの人は、この数式を見ても記号ばかりで意味がわからないと感じるでしょう。
実際この中で私たちに馴染み深い数字は\({-1}\)だけです。
では、他の記号の部分はなんなのでしょうか?
まず、\({\pi}\)は\({-1}\)に次いで、私たちには馴染み深いものでしょう。
これは言わずと知れた円周率で、きちんと数字で書こうとすると
$$
\pi = 3.14159265359…
$$
と、小数点以下の数字が無限に続いていきます。
スパコンの性能を試す際に何京桁まで計算できました、なんて話題を聞くことがある通り、この円周率\({\pi}\)はどこまで計算しても終わることなく無限に桁が続いていきます。
次に\({e}\)ですが、これはネイピア数とか自然対数の底などと呼ばれる数学の定数です。
定数というのは決まった値を持っていて計算の中で変化することのない数字のことです。なので\({\pi}\)も定数です。
ただこの\({e}\)も計算すると
$$e = 2.718281828459…$$
と無限に小数点以下の数字が続いてしまって終わることはありません。
こうした\({\pi}\)や\({e}\)のような数字は無理数と呼ばれています。
これは「もうマジ無理…」と使うような無理ではなく、理(ことわり)が無い、つまり法則やルールがないという意味で、小数だけでなく分数でも表現することができない数字を指します。
じゃあ\({\dfrac{1}{3}}\)は無理数じゃないの? というと\({\dfrac{1}{3}}\)は無理数ではありません。これを計算すると
$$
\dfrac{1}{3} = 0.33333…
$$
と確かに無限に数字が続きますが、ここにはずっと\({3}\)が繰り返し続くという法則が存在しています。こうした数字は無理数になりません。
\({\pi}\)や\({e}\)は、小数点以下の数字がどこまで言っても全く法則なく続いていて、分数でも表現することができないのです。
そして最後に\({i}\)ですが、これは虚数と呼ばれる数字です。
虚数とは2乗すると\({-1}\)になる数字を意味しています。ただ誰もが知る通りマイナスとマイナスを掛けると答えはプラスになってしまいます。
プラスとプラスを掛けても当然答えはプラスです。
2乗というのは同じ数字をニ回掛けるという意味ですから、普通に考えた場合なにをどうやっても2乗して\({-1}\)になる数字というのはありません。
ただ、計算上2乗して\({-1}\)になる数字は存在すると非常に便利だったため、数学のルールとして、2乗すると\({-1}\)になるという想像上の数字を人類は作り出したのです。
そのためこの数字は英語ではimaginary number(イマジナリーナンバー)と呼ばれます。つまり虚数\({i}\)は数学者にとってのイマジナリーフレンドみたいな数字です。
ここまでの話を聞いて、おそらくほとんどの人は、数式に含まれる記号がどういう値なのか説明されてもよくわからないと感じているでしょう。
しかしそこが重要な点です。
世界で最も美しい数式に含まれる数字たちは、この世界でまともな形で表現できないものばかりなのです。
私たちに馴染みのある\({0}\)~\({9}\)の数字で表現できない不思議な数字。それは何を意味しているのでしょうか?




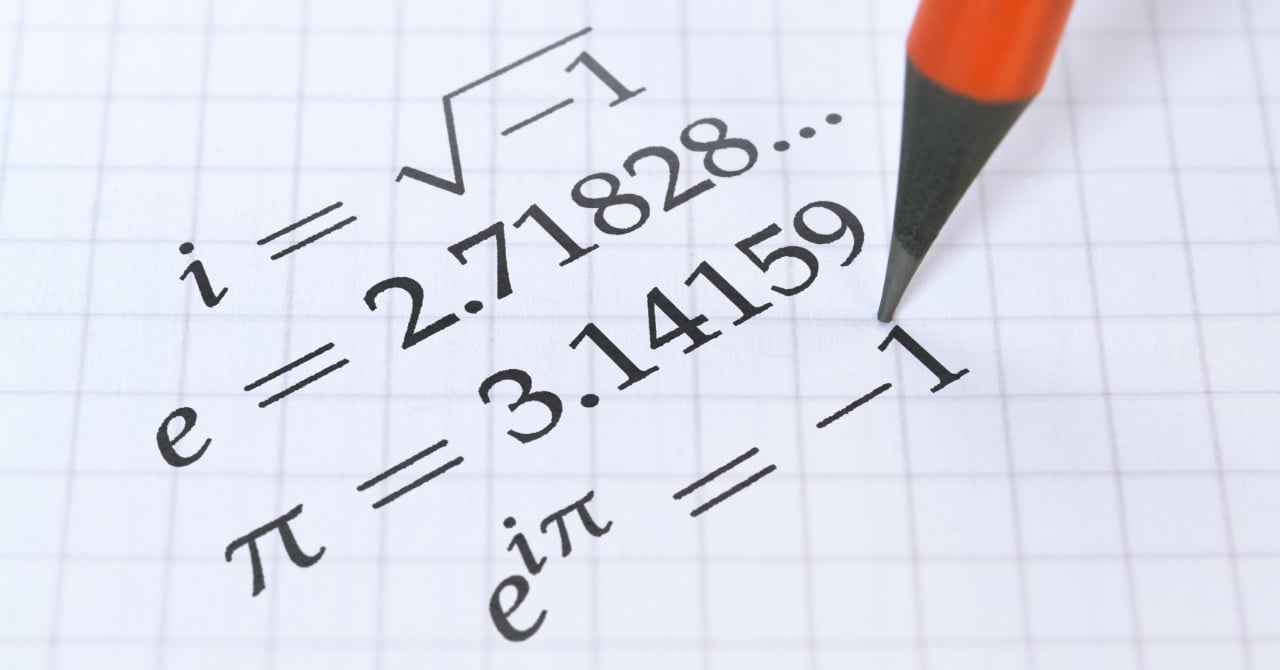

























![大人のさらさ 洗濯洗剤 ジェル 1900g シルクエッセンス効果で高保湿 ホワイトティー&フローラルの香り 詰め替え [大容量]](https://m.media-amazon.com/images/I/41G92luj2YL._SL500_.jpg)


![[コロンブス] キレイな状態をキープ アメダス 撥水・防水・防汚スプレー420mL](https://m.media-amazon.com/images/I/31-OcmTs2LL._SL500_.jpg)




![エレコム スマホ 防水ケース お風呂 IPX8 水深10m 吸盤付き [ iPhone 16e / 16シリーズ / 15シリーズ / 14シリーズ /SE3 など、6.9インチ以下のスマートフォン対応] ホワイト P-WPSB04WH](https://m.media-amazon.com/images/I/31kbvYgtI7L._SL500_.jpg)




















