\({\pi}\)(パイ)はなぜ無限に桁が続いてしまうのか?
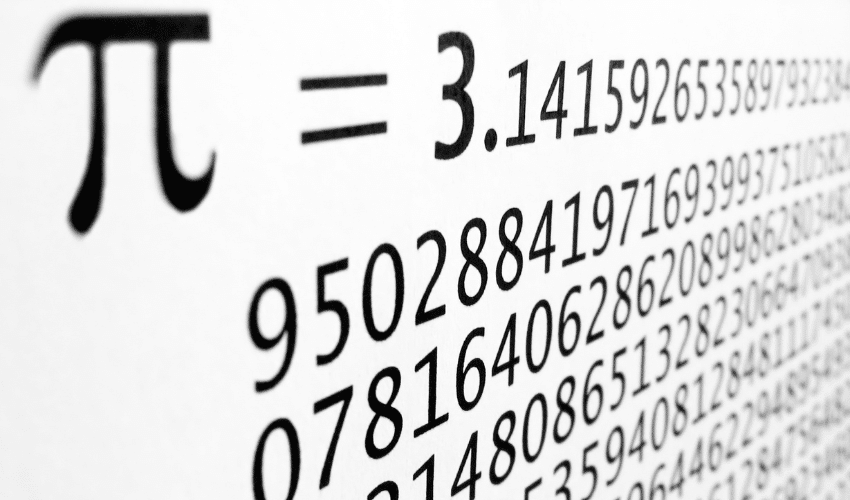
円周率\({\pi}\)についてなぜ桁が無限に続いてしまうんだ? と考えたことのある人は多いでしょう。
それは何か数学の欠陥なんじゃないかと思った人もいるかもしれません。
ではその理由について考えてみましょう。
この記事を含め、私たちは自分の気持ちを相手に伝えるとき言葉を使います。
感動したこと、感謝の気持ち、好きだという気持ち、そうした私たちの心の中の気持ちは確かにこの世界に存在しているものです。
しかしそれを誤解なく、すべて言葉だけを使って完璧に表現することはできるでしょうか?
無限に言葉を連ねたら、すごく近いことは言えるかもしれません。でもそれはきっと自分の心の中を完全に表現したものではないはずです。
円周率\({\pi}\)やネイピア数\({e}\)は、それと同じことです。
概念としての存在はみんな理解しているけれど、それを伝えるための適切な言葉はないのです。
だから、私たちがよく知る\({0}\)~\({9}\)までの数字でなんとか伝えようとすると、無限に繋げていけばすごく近いことは言えるけど、完全には表現できないものになってしまったのです。
それは私たちが、親や恋人にすごく感謝しているよとか、大好きだよという気持ちを上手く伝えきれずにもどかしい思いをしているのと同じです。
手紙を書くときにいろいろ言葉を選んだけれど、結局上手く書けなかったという経験は誰にでもあるでしょう。

世界で最も美しい数式に並ぶ記号たちは、すべて確かにこの世界にある数字です。けれど綺麗に言葉では伝えられない、無限に続けても近いことしか言えないものばかりです。
なのに、そんなもどかしい思い、不確かな思いをいろいろこね回していたら、ぴたりと綺麗に表現できた。
世界でもっとも美しい数式の美しさとは、その感覚に近いものです。
なんの法則もなく既存の数字で表現できなかった無理数たち。それがきれいに1つの\({-1}\)という整数に収まってしまった。
それはきっと誰かに気持ちが上手く伝えられなくてもどかしい思いをしている人ほど、それがシンプルに、でも完璧に伝えられたとき、その事実に感動するでしょう。
数学者は複雑なことをいかにシンプルに示すことができるかという点に、この世の美しさと神秘を感じています。
数学者たちはずっとこの不確かな概念上の数字をどうやって表現していくか悩んでいたはずです。
でもそれはこんなシンプルな式で、1つの整数として表現できました。
だからこそ、これは世界で最も美しい数式と呼ばれているのです。
もう一度、あの数式を見てみましょう。
$$
e^{i\pi} =-1
$$
どうでしょう? この数式がとても美しいと感じられるようになりましたか?




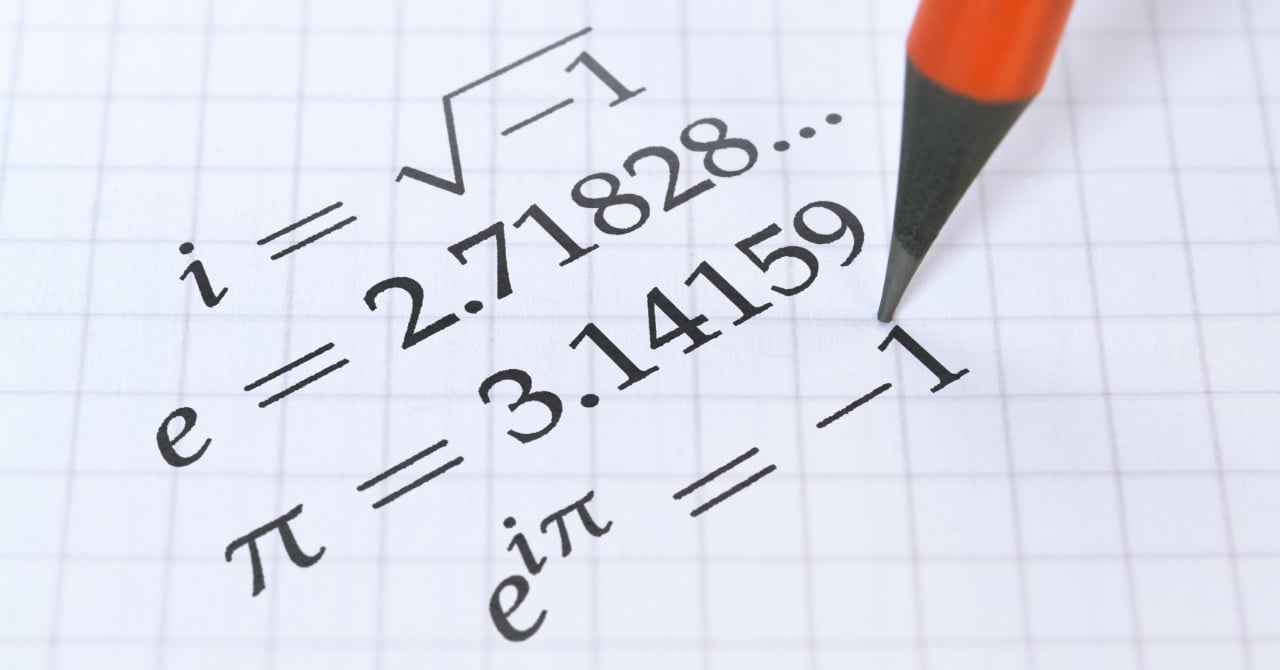

























![大人のさらさ 洗濯洗剤 ジェル 1900g シルクエッセンス効果で高保湿 ホワイトティー&フローラルの香り 詰め替え [大容量]](https://m.media-amazon.com/images/I/41G92luj2YL._SL500_.jpg)


![[コロンブス] キレイな状態をキープ アメダス 撥水・防水・防汚スプレー420mL](https://m.media-amazon.com/images/I/31-OcmTs2LL._SL500_.jpg)




![エレコム スマホ 防水ケース お風呂 IPX8 水深10m 吸盤付き [ iPhone 16e / 16シリーズ / 15シリーズ / 14シリーズ /SE3 など、6.9インチ以下のスマートフォン対応] ホワイト P-WPSB04WH](https://m.media-amazon.com/images/I/31kbvYgtI7L._SL500_.jpg)




















日常生活から考えれば、冪乗の指数に有理数でない数が入るのは人の理解を超えた途方もない話なのだが、形式的に複素数を指数にしていいのだと認めてしまえば、後は式の変形を何度もやればこの数式がポンと出てくる、はず