数式とは優れた詩

変数だからという場合を除いても、多くの数式は本来数字を書くべき場所が記号で表現されていることが多くあります。
今回の主役となっている式にも、数字はほとんどなく記号ばかりです。
記号じゃ計算できないよ、と思う人もいるかもしれません。確かに学校の数学の授業は計算ばかりさせるため、数学とは計算するものだと思っている人が多いかもしれません。
しかし計算というのは数式の使い道の1つでしかなく、実際のところ数学は計算することが目的の学問ではありません。
数学は見えない抽象的な概念を表現する学問で、数式とはある種の文章であり、詩なのです。
この世界に確かに存在する円周率\({\pi}\)やネイピア数\({e}\)、虚数\({i}\)が、私たちのよく知る\({0}\)~\({9}\)までの数字で表現できないのは、これらの数字が\({0}\)~\({9}\)の数字が作られた時代より、もっとずっと後に見つかった新しい数字だからです。
\({0}\)~\({9}\)という数字はいわば、数学における言葉のようなものです。新しく見つかった数字たちは、古来からある言葉ではピッタリの表現が見つからなかった新しい言葉なのです。
ここで、少し話題を変えて私たちが普段から使う言葉というものについて考えてみましょう。
私たちの使う言葉も時代によって変化していき、新しい言葉がどんどん追加されていきます。
それは私たちが新しく発見した概念を表現するのに、ちょうどいい言葉がなかったためです。
例えば「愛」という言葉は、現代では英語のLOVEという意味で使われていますが、実はLOVEに該当する概念は、明治頃の日本には存在していませんでした。
もちろんLOVEが示す気持ちを日本人が知らなかったわけではありません。しかしこの概念を表現する言葉は持っていなかったのです。
江戸時代は「愛してる」なんて表現はなかったのです。
そのため「I LOVE YOU」を日本語にどう翻訳したらいいでしょうか? と学生に聞かれた夏目漱石は「月が綺麗ですね」でいいんじゃないですか? と洒落たことを言ったのです。
最終的にLOVEは、仏教用語の「愛」という文字を当てて表現することになりました。これは円周率を\({\pi}\)というギリシャ文字で表現しようと決めたのに近い感覚です。




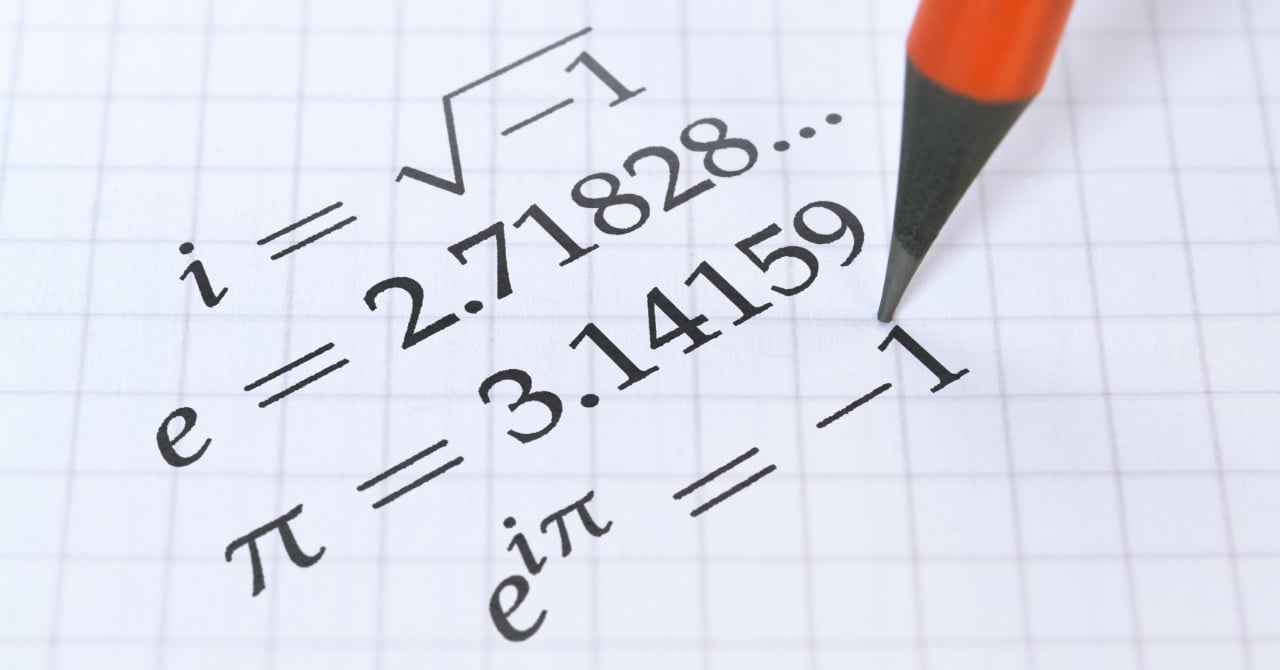

























![大人のさらさ 洗濯洗剤 ジェル 1900g シルクエッセンス効果で高保湿 ホワイトティー&フローラルの香り 詰め替え [大容量]](https://m.media-amazon.com/images/I/41G92luj2YL._SL500_.jpg)


![[コロンブス] キレイな状態をキープ アメダス 撥水・防水・防汚スプレー420mL](https://m.media-amazon.com/images/I/31-OcmTs2LL._SL500_.jpg)




![エレコム スマホ 防水ケース お風呂 IPX8 水深10m 吸盤付き [ iPhone 16e / 16シリーズ / 15シリーズ / 14シリーズ /SE3 など、6.9インチ以下のスマートフォン対応] ホワイト P-WPSB04WH](https://m.media-amazon.com/images/I/31kbvYgtI7L._SL500_.jpg)




















