数学により物理学の3つの主要理論を統合することに成功 (2/3)

ヒルベルト第六問題ついに崩れる：粒子から台風まで“一本の数学的鎖”で貫通

研究チームは、このミクロからマクロへの橋渡しを二段階のアプローチで実現しました。

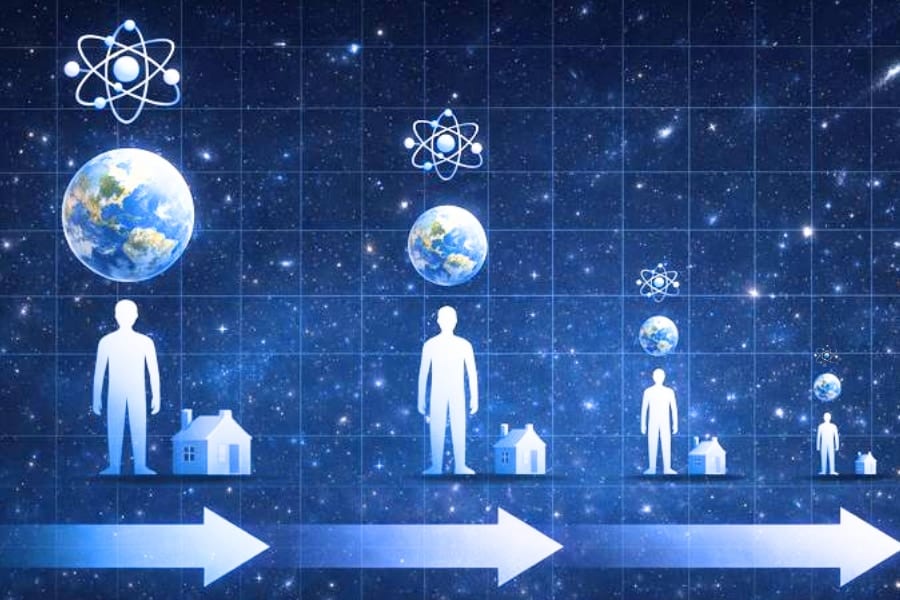
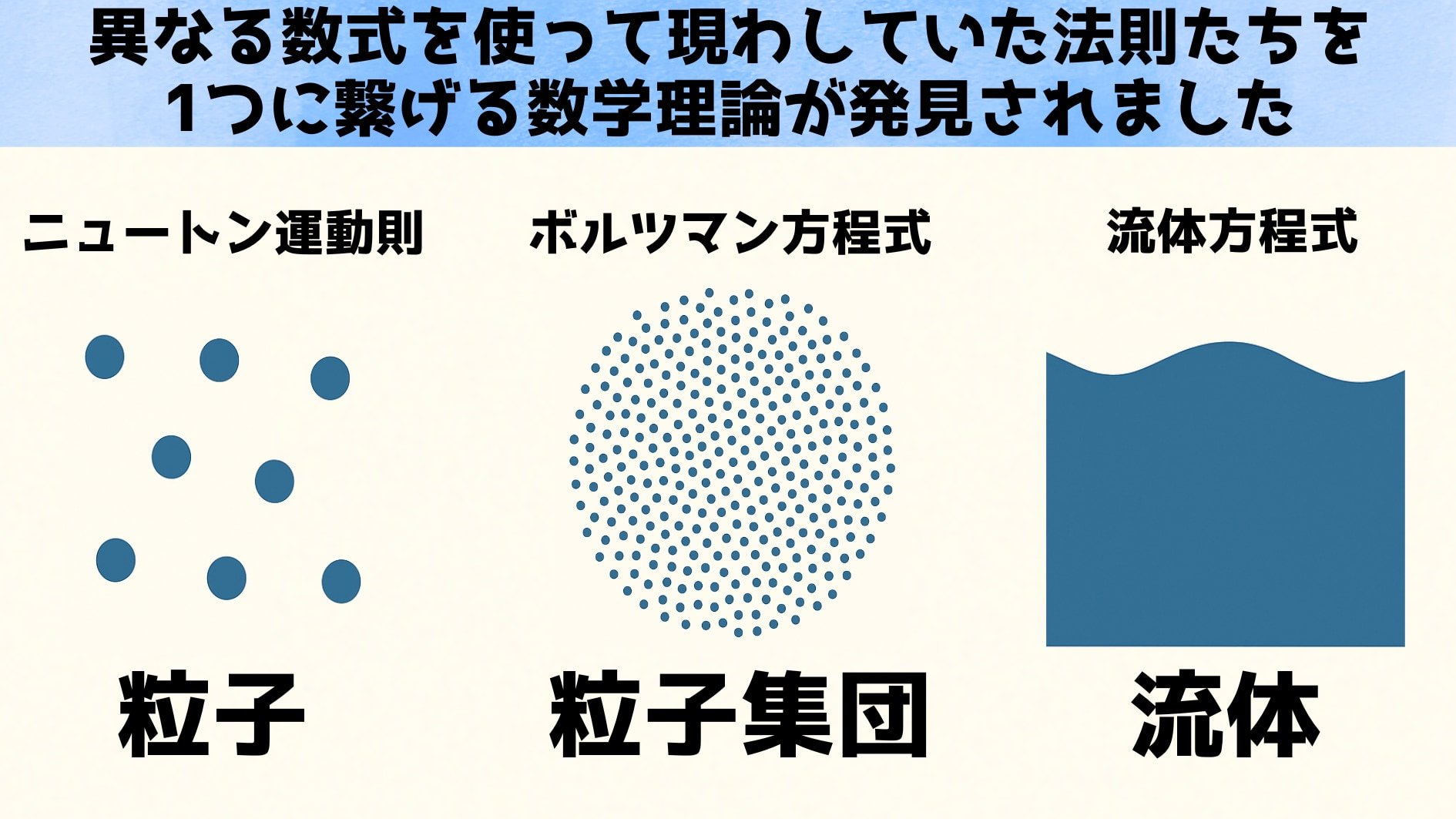
ニュートンの粒子力学（左）からボルツマンの運動論的方程式（中間）を経て、流体力学の方程式（右）へと至る論理の連鎖。

今回の研究では、この図に示されたミクロ→中間→マクロのすべての段階を一貫して証明した。

ミクロから中間（ニュートン力学 → ボルツマン方程式）

まず研究チームは、無数の粒子が飛び交い衝突するミクロな系から、ボルツマン方程式という統計的な記述が現れることを証明しました。

彼らが扱ったのは、直径が極めて小さい硬い球（ビリヤード玉のような粒子）同士が弾性的に衝突する理想化された気体模型です。

粒子数を非常に大きく、粒径を非常に小さくとる極限（ボルツマン・グラッド極限と呼ばれます）では、粒子の衝突頻度が一定に保たれつつ、粒子系全体の確率的振る舞いがボルツマン方程式の解に収束することを示しました。

直感的に言えば、「粒子が無数に存在すると仮定すれば、典型的な粒子の振る舞いはボルツマン方程式で記述できる」ことを数学的に裏付けたのです。

このステップ自体は古くから物理学者が考えてきたもので、1970年代にオスカー・ランフォードによってごく短い時間については証明されていました。

しかし長時間にわたって成り立つことを厳密に示すのは困難で、衝突を繰り返すうちに粒子の運動がどれだけ複雑になってもボルツマン方程式が成り立ち続けるのか、誰も証明できずにいたのです。

今回Deng氏らのチームは、新しい数学的手法を駆使して粒子衝突の履歴を厳密に追跡し、その累積効果が無視できるほど小さいことを示すことで、この長年の難関を突破しました。

難しく聞こえるかもしれませんが、「たとえ無数の衝突を経ても、粒子たちの振る舞いは統計的な平均像から大きく逸れない」ことを保証したと言えばイメージしやすいでしょう。

こうして任意の長時間スケールでニュートン力学からボルツマン方程式を導けるという、大きな一歩が達成されたのです。

中間からマクロ（ボルツマン方程式 → 流体力学方程式）

次に研究チームは、得られたボルツマン方程式から従来の流体力学の方程式（マクロの方程式）を導くことに取り組みました。

この部分は物理学・数学の分野では「流体力学極限」として知られ、過去の研究で多くの成果が蓄積されています。

気体分子の平均自由行程（衝突と衝突の間の距離）がゼロに近づく、つまり衝突頻度が極めて高くなる極限では、粒子の集団は滑らかな流体のように振る舞います。

このときボルツマン方程式から導かれるのが、オイラー方程式やナビエ–ストークス方程式といった流体の方程式です。

Deng氏らはこの極限操作を厳密に行い、2種類の基本的な流体方程式をニュートン力学から導出することに成功しました。

一つはインクームプレッシブル・ナビエ–ストークス–フーリエ方程式と呼ばれるもので、粘性のある流体（空気や水など）の流れと熱の伝わりを記述する式です。

もう一つは圧縮性オイラー方程式で、粘性を無視できる流体（例えば音波や衝撃波のような気体の運動）を記述します。

これらはいずれも工学や自然現象の解析に日常的に使われている基本方程式です。

以上の二段階を組み合わせることで、研究チームはニュートンの粒子論から連続体の流体方程式までを一直線に結ぶことに成功しました。

言い換えれば、「微視的な世界の法則から巨視的な世界の法則を導けることを示した」ことになります。

これはヒルベルトが19世紀末に夢見た課題を正面から射抜いた、歴史的偉業と言えるでしょう。