「フェルマーの最終定理」をめちゃくちゃ簡単に説明する

「私はこの命題について、真に驚くべき証明を見出したが、それを記すにはここはあまりに余白が足りない」
360年前、フランスの数学者ピエール・ド・フェルマーはたったこれだけのメモを問題の脇に書き残してこの世を去ってしまった。
このツイッターにも投稿されていそうなフェルマーのメモは大変話題になり、以後この命題は「フェルマーの最終定理」と呼ばれることになる。
「フェルマーの最終定理」は、一見すると義務教育で教わる「ピタゴラスの定理」の拡張版だ。なんだか簡単に解けそうな問題にも見える。
この命題の「n=2」の場合が、直角三角形の辺の長さを求めるいわゆる「ピタゴラスの定理(三平方の定理)」である。
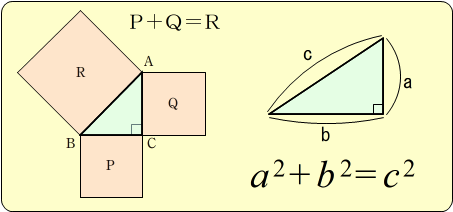
しかし「n」が2なら無限に解が存在するというのに、この「n」が3以上の数字になると「x,y,z」を満たす解は一切存在しなくなってしまう。これがいわゆる「フェルマーの最終定理」の命題だ。
この問題を最終的に解いたアンドリュー・ワイルズは10歳の頃、図書館でこの問題を見つけて「俺なら解けるんじゃね?」と思ったようだ。それはそれでとんでもないお子様だが、しかしこれが大きな罠だった。
「n」が3以上の場合というのは、つまり無限に存在する「n」について、それぞれ解が無いと証明しなければならないわけで、これは非常に困難な証明なのだ。
以後30年以上、ワイルズはこの問題の呪縛に捕らわれることになる。






























![[W.P.S.] 防水スプレー 除菌 抗菌 防汚 機能付き 大容量420ml 日本製](https://m.media-amazon.com/images/I/41aHfy9uuZL._SL500_.jpg)
![よーく聞いてね!3つのヒントで学ぶ!どうぶつカード ([バラエティ])](https://m.media-amazon.com/images/I/51zT3OcliFL._SL500_.jpg)




























