カオス現象は、なぜ「予測できない」のか
カオス現象とは、一言で表せば「何が起こるか予測できない」現象です。
この部分を、科学史と共にもう少し具体的に紐解いていきます。

1687年にアイザック・ニュートンは著書『自然哲学の数学的諸原理』において運動の第2法則を発表しました。
運動の第2法則は以下のような主張でした。
- 物体の運動状態の時間変化が、物体に作用する力に比例する
- 物体の運動状態の時間変化が、物体に作用する方向と同じになる
この法則からニュートンの運動方程式が導かれるため、高校で物理を習った人は、$$m\boldsymbol{a}=\boldsymbol{F}$$という式の形でこの法則を知っているかもしれません。
この運動方程式の出現によって斜面を転がる石や空から降ってくる雨などの自然現象、さらには天体の動きまでも説明できるようになりました。
もはや運動方程式によって、この世の全てが説明できるのではないかとさえ思えてしまうかもしれません。
実際こうした中、「一番最初の状態とそれが時間の変化でどのように変わるかを記述する法則さえ得られれば、あらゆる未来の状態が予測できる」という考え方が現れました。
これを決定論と言います。
決定論的な世界観では、どんな複雑な事象でもその事象を記述する式が解明されれば必ず未来の状態を予測できるようになる、と考えられていました。
もし本当にそうであれば、世界の様々な問題は今よりもずっと少なくなっていたでしょう。
もちろんそんなに事は上手く行きませんでした。
その後決定論的な見通しを否定するような事象が次々と現れたのです。
カオス現象もその一つでした。
カオス現象とはその名の通り非常に混沌とした現象を指します。
「混沌とした現象」とは、考慮するべき要因があまりに多く、しかもそれらが非常に複雑な振る舞いをするため、数学的に記述することが困難な現象のことです。
例えば1つのボールならその運動を単純な式で記述でき、簡単に解くこともできるため未来の状態を予想できます。
しかし大気や液体は大量の粒子の集団なので、その動きを予測しようとした場合、含まれる粒子それぞれの及ぼす影響を考慮しなければなりません。
これを式にして解こうとすると、一気に難易度が跳ね上がってしまいます。
とはいえ、カオス現象を見せる全ての式そのものが複雑というわけではありません。
中には簡単な式で振る舞いを記述できるものもあります。
しかし、ある程度の時間が経ったあとの振る舞いが極めて複雑になってしまうと、もはや解けない式となってしまい予測不能であると表現されます。
そのわかりやすい一例が、ロジスティック写像です。
ロジスティック写像はイギリスの数理生物学者であるロバート・メイの研究を発端にして、生物の個体数が世代を経て変化していく様子を表す式として世に広まりました。
これは次の二次関数で簡単に表すことができます。
$$y=ax(1-x)$$
これはある世代における個体数を\(x\)、繁殖率\(a\)をとして次の世代の個体数\(y\)を表す式になっています。
まず定数\(a\)と変数\(x\)の値を適当に決めると、この式から\(y\)の値を得ることができます。
この\(y\)を新しく\(x\)として用いると、また新たな\(y\)を得ることができます。
これを繰り返すと、\(a\)が3以下の場合はある値に収束します。
\(a\)の値を3以上、そして段々と大きくして同じことをすると面白い現象が起こります。
下の図は、\(a\)(図中では\(r\))を変えたときに、操作の繰り返しによってどのような値(縦軸)に収束するかを示したグラフです。
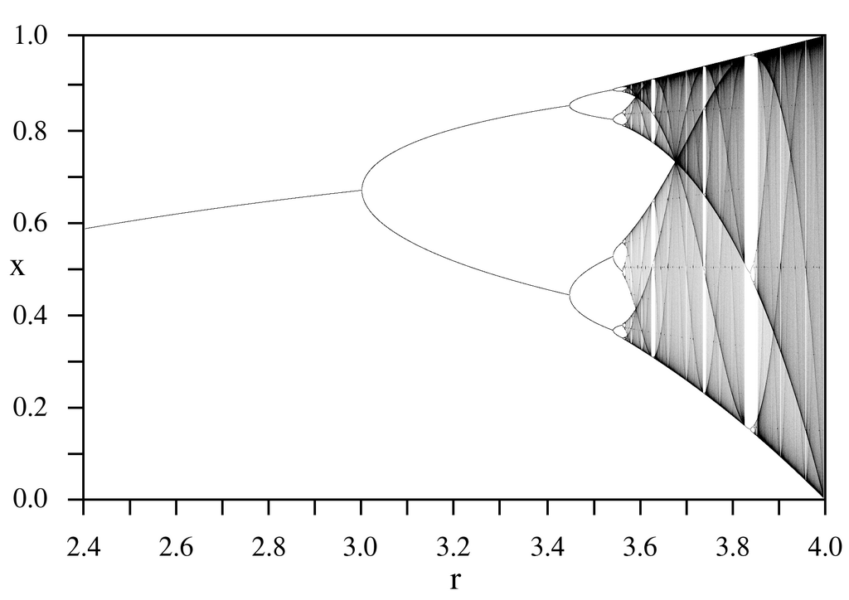
\(a\)が3を超えると、まず一つの値に収束しなくなり複数の値を交互に取るようになります。
そして\(a\)が3.56995を超えると\(y\)の最終的に取る値が極めて複雑になり規則性が見られなくなるのです。
この境界値3.56995はファイゲンバウム点と呼ばれています。
このように、カオス現象における予測できないというのはランダムであるという意味ではありません。
ロジスティック写像のように関係式は非常に単純でも、ある\(a\)における未来の\(y\)の値を書き表すことは非常に困難です。
この複雑さを指して、予測できないという表現をしているのです。
そうは言っても、近似値で良いから具体的な値が欲しいことも実用上はあります。
その場合はコンピュータによる数値解析が行われるのが一般的です。
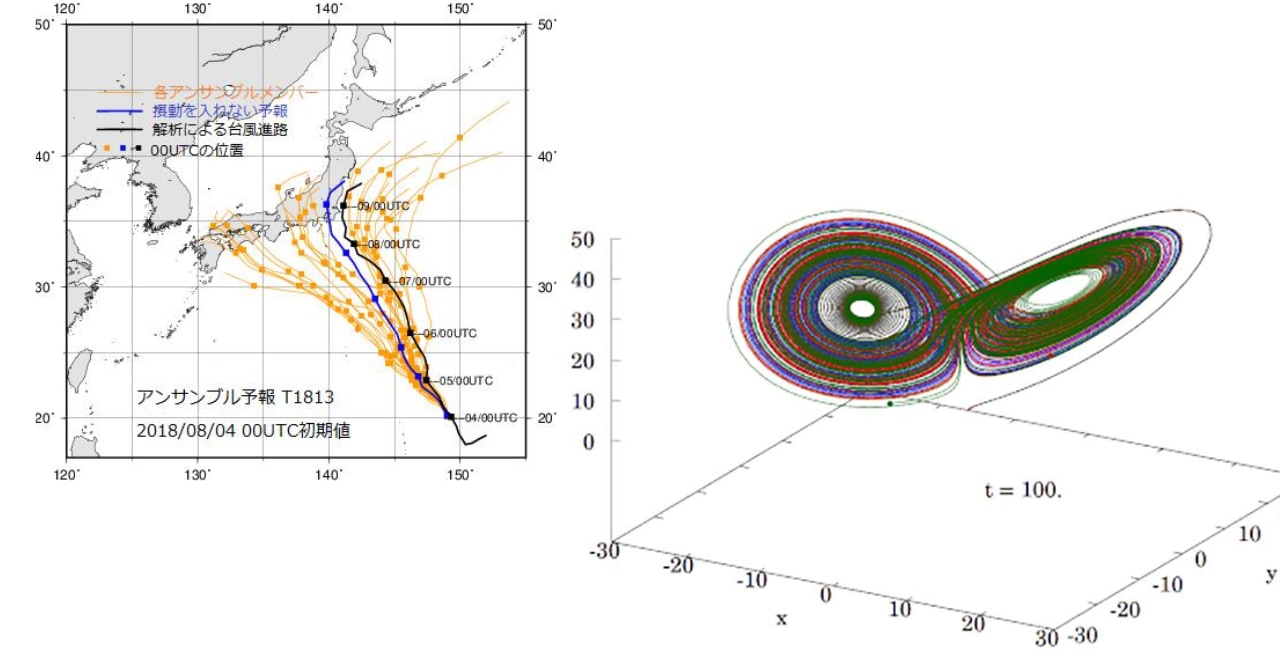
しかし、今見たように\(a\)がファイゲンバウム点を超えたあとは\(a\)をごくわずかに変えただけでも未来の\(y\)の値には大きな変化が生じます。
そしてコンピュータといえども無限の桁数を扱えるわけではないため、真の値とは必然的に誤差が生まれます。
さらにその誤差は計算を繰り返せばどんどんと増幅されていきます。
その結果得られる値は、もはや真の値からはかけ離れたものになっているでしょう。
こうした理由により、予測は事実上不可能になるのです。



























![[W.P.S.] 防水スプレー 除菌 抗菌 防汚 機能付き 大容量420ml 日本製](https://m.media-amazon.com/images/I/41aHfy9uuZL._SL500_.jpg)
![[WILL CLENS] シューズパウダー 日本製 無香料 シューケアキット 靴 消臭 パウダー (1本)](https://m.media-amazon.com/images/I/41m8Ig2XigL._SL500_.jpg)
![よーく聞いてね!3つのヒントで学ぶ!どうぶつカード ([バラエティ])](https://m.media-amazon.com/images/I/51zT3OcliFL._SL500_.jpg)