AIが10万個の方程式で表された複雑な量子問題を4つの方程式に統合！
人類はその優れた知能によって、これまで数々の物理法則を発見し、その理解は日常生活の常識を超越した、奇妙な量子世界にも及ぶようになりました。
この偉大な成果は人類の創造性を源泉としているものの、理論を表現するツールとしての方程式の存在も不可欠となっています。
電子や光子のふるまいや運動法則を「方程式」の形で表記することで、電子や光子の本質を、口頭での百聞に勝る正確さで理解することが可能になります。
しかし「メイド イン 人類脳」の方程式には大きな問題がありました。
その代表としてあげられるのが、複数の電子が相互作用する場合（多体量子問題）です。
奇妙な量子世界の住人である電子には、粒子としての性質と波としての性質があるだけでなく、他の多くの電子と相互作用を起こし、たとえ離れた場所にあったとしても、互いの運命が絡み合う複雑な状態（量子もつれ）を引き起こします。
人類製の方程式を使うことでも、この複雑な状況を表記することは可能です。
しかし扱う電子の数が増えるにつれて、状況を表記するために必要とされる方程式の量と相互作用によって生じる複雑さは爆発的に増加していきます。
このような膨大な計算は既存のコンピューターで処理することは非常に困難であり、これまで唯一の解決策は量子コンピューターの使用であるとされていました。
しかし残念なことに現実的な量子コンピューターの普及は少なくとも数年から十数年後であると考えられています。
そこで今回、フラットアイアン研究所の研究者たちは、AIのニューラルネットに方程式を圧縮する方法を学習させることで、膨大な量の方程式を、数個の式に変換できないかを試すことにしました。
実験にあたっては、複数の電子の相互作用をモデル化するための格子状のネットワーク構造（ハバードモデル）が用意されました。
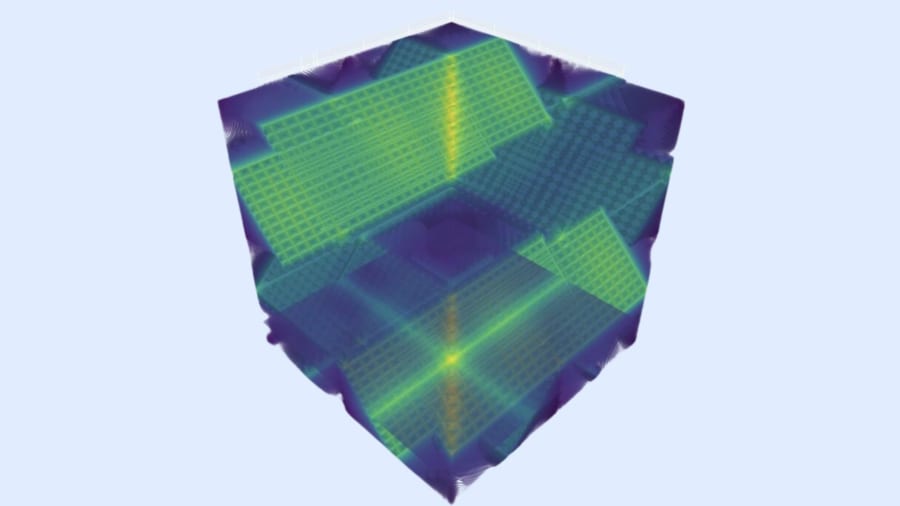
また研究では、このモデルを視覚的にとらえるために、数学的な概念に従った方程式たちのビジュアル化が行われています。
図はぱっと見では、内部が透けたサイコロのように見えますが、図の表記に使われる1つの画素が1つの方程式を記しており、実験に使われたモデルを正確にとらえるには、10万個の方程式（10万画素）が必要であることが示されています。
次に研究者たちは、方程式の圧縮方法を学習したAIに、これら10万個の方程式を正確さを維持したま圧縮するように命令しました。
すると最終的には、わずか4個の方程式（4画素）だけで表記可能なことが判明します。
また検証によって10万個の方程式が4個に圧縮されても、電子の挙動を表現する正確さが失われていないことが判明しました。
これら4個は10万個ぶんの方程式をまとめた膨大な内部変数を備えており、人類の脳では生成不可能な「メイド イン 機械脳」な方程式と言えるでしょう。
