重力が強いと時間が歪む？ 一般相対性理論とは？
よく耳にするけど、よくわからない代表理論といえば一般相対性理論でしょう。
今回の研究成果の意味を伝えるために、まずはこの相対性理論の解説から初めましょう。
相対性理論は、言わずと知れた物理学者アルベルト・アインシュタインが発表した物理理論です。
この理論のもっとも重要な主張は、光速度は何があっても世界で絶対普遍の定数であると言うことです。
光は、この世界のどこから見ても、どんな状況で見ても、絶対に秒速30万kmという速度で進んでいます。
ふーん、と聞き流してしまいそうですが、これには世界を歪ませる重要な意味があります。
例えば光の速度で移動する宇宙船を考えてみましょう。その中で進行方向に向かって手鏡を掲げた場合、鏡はどうなるでしょう？
光速で移動していたら、顔から放たれる光は永遠に鏡に届かないことになってしまいます。それどころか、進行方向と逆方向を向いたら、何も見えないということになってしまいます。
これだと、光速の宇宙船に乗っている人からは光の速度が0に見えるということになります。あれれ？ おかしいな？ となりますね。
光がどんな状況から見ても一定速度という状態を実現するためには、光速で移動している人にも、止まっている人にも光の速度が一定に見えなければなりません。
学校で習った相対速度を無視しなければならないのです。
果たしてそんなことが可能なのでしょうか？ アインシュタインはこの方法を考え、そして1つの答えを見出しました。
光の速度が移動している場合でも、止まっている場合でも、常に一定に見えるためには、時間の方を歪めてしまえばいいのです。
小学校で「はじきの法則」というものを教わったことを覚えているでしょうか？ 速度は、進んだ距離を時間で割れば導けます。
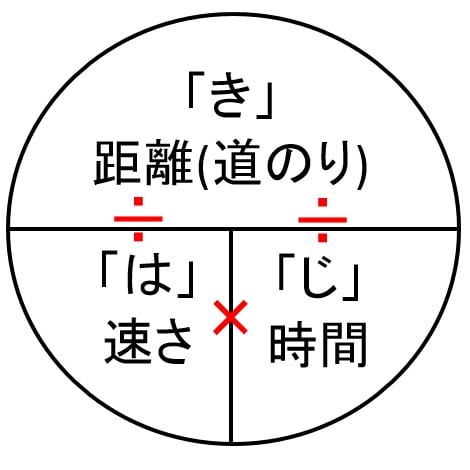
もし、この法則の中で、速度だけを定数にして扱おうとするなら、時間と距離だけ変えてしまえばいいのです。
私たちから見たら、時間は絶対普遍のものに思えますが、自然にとっては、時間なんかより光の速度を一定に保つことのほうがずっと優先度が高い問題です。
光の速度が変わるくらいだったら、時間と長さを歪めてしまえというわけです。
よく、光速を超えて運動することは不可能と言いますが、それもこのことが原因です。
もし光速を超えて運動してしまうと、自然は光速度を保つために、そいつの周りに流れる時間を巻き戻してしまうのです。光速を超えたらタイムマシンができる、というのもこの原理によるものです。
つまりは、光の速度を一定に保つためなら、時間も空間も歪めていいというのがアインシュタインの特殊相対性理論なのです。
そういえば、相対性理論には特殊相対性理論と一般相対性理論があったよね？ どう違うの？ と言う人もいるかもしれません。今回の時計の話も一般相対性理論の効果だと言われています。
特殊というのは、今の問題を、物体が等速直線運動した場合のみに限定して考えているためです。
現実とは異なる特殊な条件を加えて、物事を単純化して考えた場合、それを特殊理論と呼びます。
物理の問題で「ただし、摩擦は考えないものとする」なんて但し書きを見た覚えがあると思いますが、こういう現実と異なる特殊な条件を付与して考える問題がいわゆる特殊理論です。
なので、こういう特殊な条件を用いないで、現実にそのまま当てはめても成立するようにしようというのが「一般理論」になります。
物理問題の例でいうなら、「摩擦も考慮して答えなさい」というのが一般理論です。
お、難しそう、と言う感じがしますね。このため、特殊相対性理論に比べて、一般相対性理論の方が、内容はぐっと難しいものになります。
一直線の等速運動で考えていた特殊相対性理論を、私たちが暮らす4次元時空（3次元空間+1次元時間）に適用したのが一般相対性理論なのです。
確かに難しいですが、単純に行ってしまえば、速度の問題で伸び縮みしていた時間が、重力でも伸び縮みするよ、というのが一般相対性理論の内容です。
では重力とは何でしょう？
アインシュタインはこれを時空間の歪みであると説明しました。
世界をゴムシートで出来た2次元平面と考えた場合、ここにボーリングの玉を乗せると大きくたわんで、周りの小さなビー玉などを吸い寄せます。
このシートのたわみが重力による時空の歪みに相当するものです。
では、このたわんだゴムシートの表面を光が通った場合どうなるでしょう？
ピンと張った状態のときと比べて、たわんだ状態では光が通る距離は長くなってしまいます。
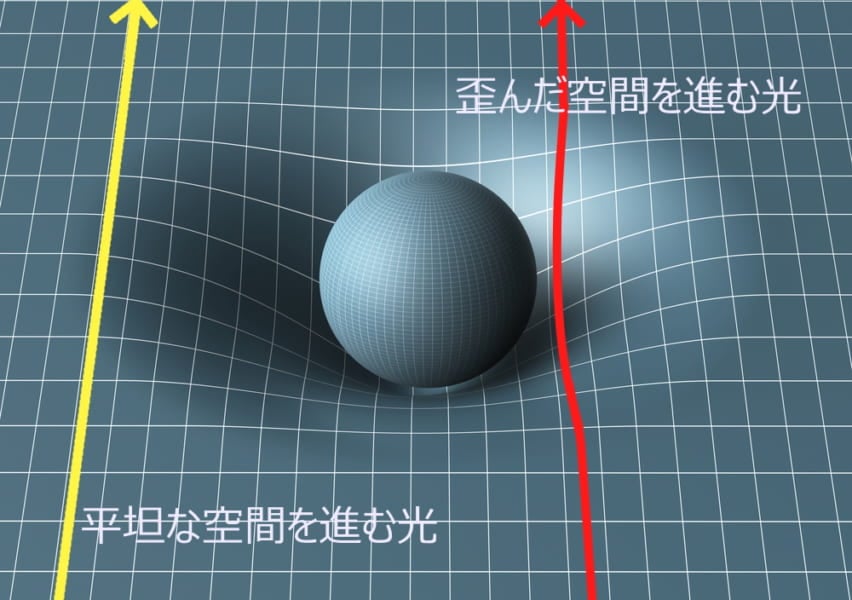
しかし、この場合でも2つの光は同じ速度にならなければなりません。そのため、重力で歪んだ空間では、光の速度を保つために、時間の流れが遅くなってしまうのです。
これが、簡単に行った場合の一般相対性理論です。
