月が離れる原因は、自転と公転の速度差
ここでポイントとなるのは、地球の自転速度と月の公転速度の差です。
地球は誰もが知る通り24時間で1回自転しています。
一方、月は地球の周りを27.3日かけて1周します。
当然のことながら、地球の自転速度のほうが、月の公転速度よりずっと速い状態です。
ここでちょっと困ったことが起こります。
さきほど、地球の海は潮汐力で膨らんでいると話しましたが、この膨らんだ部分は地球の自転が速いために、月の正面よりややズレた位置に移動してしまうのです。
しかし、月と地球の重力的な影響は、この潮汐力で膨らんだ部分で繋がっているので、先行した膨らみは月を引っ張ってその公転速度を加速させます。
一方、月は膨らんだ海を引っ張って、地球の自転を減速させていきます。
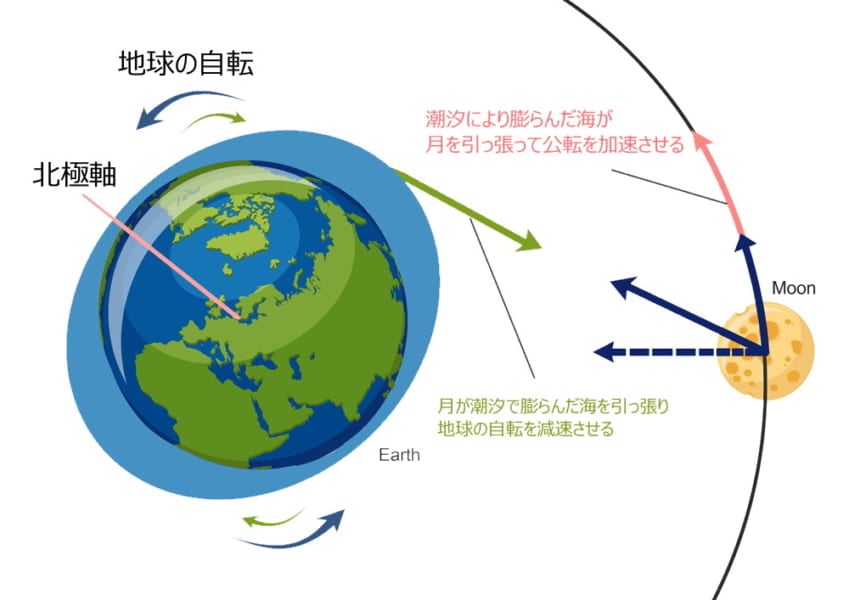
そう、実は地球は月の影響で自転速度がどんどん減速していて、逆に月は公転速度をどんどん加速させているのです。
この影響で、地球の1日は10万年で1秒ほどの長くなると考えられています。
しかし、月は単純に公転速度を増やしていくことはできません。月が地球から一定距離を保ち続けるためには、安定した公転速度があるのです。
そこで、月は公転速度を上げる代わりに、公転軌道を広げていきます。
この現象は、角運動量保存の法則によって説明することができます。
角運動量保存の法則は、フィギアスケートの選手の動きを思い出すとイメージしやすいでしょう。
フィギアスケートの選手は、腕を広げているときはゆっくり回転しているのに、腕を内側に引き込んで体を縮めると、どんどん回転が加速していきます。
選手の腕の位置を、月の公転軌道として考えると、地球に近いほど速く回転して、離れるほどゆっくり回転することになります。
角運動量は回転半径、運動する物体の質量,回転速度の3つの値の積なので、このとき、角運動量は常に一定です。

つまり、外から力を受けて月の角運動量が増えた場合、物理的には公転速度を増やしても、公転半径を広げても、どっちでもいいのです。
このため、地球の自転に引っ張られた月は、一定の速度で地球の周りを公転し続けるために、軌道を広げる方を選択しました。
こうして月は徐々に地球から離れていくことになったのです。































![大人のさらさ 洗濯洗剤 ジェル 1900g シルクエッセンス効果で高保湿 ホワイトティー&フローラルの香り 詰め替え [大容量]](https://m.media-amazon.com/images/I/41G92luj2YL._SL500_.jpg)


![よーく聞いてね!3つのヒントで学ぶ!どうぶつカード ([バラエティ])](https://m.media-amazon.com/images/I/51zT3OcliFL._SL500_.jpg)